Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T15:56:30.389Z Has data issue: false hasContentIssue false
  • English
  • Français

ZEROS OF THE MÖBIUS FUNCTION OF PERMUTATIONS

Part of: Combinatorics

Published online by Cambridge University Press:  14 August 2019

Robert Brignall ,
Vít Jelínek ,
Jan Kynčl  and
David Marchant
Robert Brignall
Affiliation:
School of Mathematics and Statistics, The Open University, Milton Keynes, MK7 6AA, U.K. email [email protected]
Vít Jelínek
Affiliation:
Computer Science Institute, Faculty of Mathematics and Physics, Charles University, Prague, Czech Republic email [email protected]
Jan Kynčl
Affiliation:
Department of Applied Mathematics, Faculty of Mathematics and Physics, Charles University, Prague, Czech Republic email [email protected]
David Marchant
Affiliation:
School of Mathematics and Statistics, The Open University, Milton Keynes, MK7 6AA, U.K. email [email protected]
Get access

Abstract

We show that if a permutation $\unicode[STIX]{x1D70B}$ contains two intervals of length 2, where one interval is an ascent and the other a descent, then the Möbius function 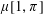$\unicode[STIX]{x1D707}[1,\unicode[STIX]{x1D70B}]$ of the interval 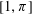$[1,\unicode[STIX]{x1D70B}]$ is zero. As a consequence, we prove that the proportion of permutations of length $n$ with principal Möbius function equal to zero is asymptotically bounded below by 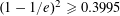$(1-1/e)^{2}\geqslant 0.3995$. This is the first result determining the value of 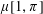$\unicode[STIX]{x1D707}[1,\unicode[STIX]{x1D70B}]$ for an asymptotically positive proportion of permutations $\unicode[STIX]{x1D70B}$. We further establish other general conditions on a permutation $\unicode[STIX]{x1D70B}$ that ensure 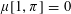$\unicode[STIX]{x1D707}[1,\unicode[STIX]{x1D70B}]=0$, including the occurrence in $\unicode[STIX]{x1D70B}$ of any interval of the form 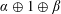$\unicode[STIX]{x1D6FC}\oplus 1\oplus \unicode[STIX]{x1D6FD}$.

MSC classification

Primary: 05A05: Permutations, words, matrices
Type
Research Article
Information
Mathematika , Volume 65 , Issue 4 , 2019 , pp. 1074 - 1092
Copyright
Copyright © University College London 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

V. Jelínek and J. Kynčl were supported by project 16-01602Y of the Czech Science Foundation (GAČR). J. Kynčl was also supported by Charles University project UNCE/SCI/004.

References

Albert, M. H. and Atkinson, M. D., Simple permutations and pattern restricted permutations. Discrete Math. 300(1-3) 2005, 1–15.10.1016/j.disc.2005.06.016Google Scholar
Albert, M. H., Atkinson, M. D. and Klazar, M., The enumeration of simple permutations. J. Integer Seq. 6(4) 2003, Article 03.4.4.Google Scholar
Atkinson, M. D. and Stitt, T., Restricted permutations and the wreath product. Discrete Math. 259(1–3) 2002, 19–36.10.1016/S0012-365X(02)00443-0Google Scholar
Björner, A., The Möbius function of subword order. In Invariant Theory and Tableaux (Minneapolis, MN, 1988) (IMA Vol. Math. Appl., 19 ), Springer (New York, 1990), 118–124.Google Scholar
Brignall, R., Jelínek, V., Kynčl, J. and Marchant, D., Zeros of the Möbius function of permutations. Preprint, 2018, arXiv:org/abs/1810.05449v1.Google Scholar
Brignall, R. and Marchant, D., The Möbius function of permutations with an indecomposable lower bound. Discrete Math. 341(5) 2018, 1380–1391.10.1016/j.disc.2018.02.012Google Scholar
Burstein, A., Jelínek, V., Jelínková, E. and Steingrímsson, E., The Möbius function of separable and decomposable permutations. J. Combin. Theory Ser. A 118(8) 2011, 2346–2364.10.1016/j.jcta.2011.06.002Google Scholar
Euler, L., Recherches sur une nouvelle espèce des quarrés magiques. Verhandelingen uitgegeven door het zeeuwsch Genootschap der Wetenschappen te Vlissingen 9 1782, 85–239.Google Scholar
Jelínek, V., Kantor, I., Kynčl, J. and Tancer, M., On the growth of the Möbius function of permutations. J. Combin. Theory, Ser. A 169 2020,105121.Google Scholar
Kaplansky, I., The asymptotic distribution of runs of consecutive elements. Ann. Math. Stat. 16(2) 1945, 200–203.10.1214/aoms/1177731121Google Scholar
Rumney, M. and Primrose, E. J. F., A sequence connected with the sub-factorial sequence. Gaz. Math. 52(382) 1968, 381–382.10.2307/3611860Google Scholar
Sagan, B. E. and Vatter, V., The Möbius function of a composition poset. J. Algebraic Combin. 24(2) 2006, 117–136.10.1007/s10801-006-0017-4Google Scholar
Sloane, N. J. A., The on-line encyclopedia of integer sequences, published electronically at http://oeis.org/.Google Scholar
Smith, J. P., On the Möbius function of permutations with one descent. Electron. J. Combin. 21(2) 2014, 19 Paper 2.11.Google Scholar
Smith, J. P., Intervals of permutations with a fixed number of descents are shellable. Discrete Math. 339(1) 2016, 118–126.10.1016/j.disc.2015.08.004Google Scholar
Smith, J. P., A formula for the Möbius function of the permutation poset based on a topological decomposition. Adv. Appl. Math. 91 2017, 98–114.10.1016/j.aam.2017.06.002Google Scholar
Smith, J. P., private correspondence, 2018.Google Scholar
Stanley, R. P., Enumerative Combinatorics, 2nd edn., Vol. 1 (Cambridge Studies in Advanced Mathematics 49 ), Cambridge University Press (Cambridge, 2012).Google Scholar
Steingrímsson, E. and Tenner, B. E., The Möbius function of the permutation pattern poset. J. Comb. 1(1) 2010, 39–52.Google Scholar
Wilf, H. S., The patterns of permutations. Discrete Math. 257(2-3) 2002, 575–583.10.1016/S0012-365X(02)00515-0Google Scholar