Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-28T04:58:41.317Z Has data issue: false hasContentIssue false
  • English
  • Français

VARIANTS OF ERDŐS–SELFRIDGE SUPERELLIPTIC CURVES AND THEIR RATIONAL POINTS

Part of: Diophantine equations

Published online by Cambridge University Press:  03 April 2018

Pranabesh Das ,
Shanta Laishram  and
N. Saradha
Pranabesh Das
Affiliation:
Stat-Math Unit, Indian Statistical Institute Delhi Centre, New Delhi 110016, India email [email protected]
Shanta Laishram
Affiliation:
Stat-Math Unit, Indian Statistical Institute Delhi Centre, New Delhi 110016, India email [email protected]
N. Saradha
Affiliation:
School of Mathematics, Tata Institute of Fundamental Research, Mumbai 400005, India email [email protected]
Get access

Abstract

For the superelliptic curves of the form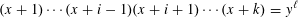

$$\begin{eqnarray}(x+1)\cdots (x+i-1)(x+i+1)\cdots (x+k)=y^{\ell }\end{eqnarray}$$
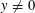with $y\neq 0$, 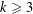$k\geqslant 3$, 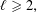$\ell \geqslant 2,$ a prime and for 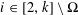$i\in [2,k]\setminus \unicode[STIX]{x1D6FA}$, we show that 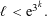$\ell <\text{e}^{3^{k}}.$ Here 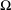$\unicode[STIX]{x1D6FA}$ denotes the interval 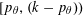$[p_{\unicode[STIX]{x1D703}},(k-p_{\unicode[STIX]{x1D703}}))$, where 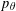$p_{\unicode[STIX]{x1D703}}$ is the least prime greater than or equal to 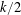$k/2$. Bennett and Siksek obtained a similar bound for 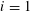$i=1$ in a recent paper.

MSC classification

Primary: 11D61: Exponential equations
Type
Research Article
Information
Mathematika , Volume 64 , Issue 2 , 2018 , pp. 380 - 386
Copyright
Copyright © University College London 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bennett, M. A., Bruin, N., Győry, K. and Hajdu, L., Powers from products of consecutive terms in arithmetic progression. Proc. Lond. Math. Soc. (3) 92(2) 2006, 273–306.CrossRefGoogle Scholar
Bennett, M. A. and Siksek, S., Rational points on Erdős–Selfridge superelliptic curves. Compos. Math. 152 2016, 2249–2254.Google Scholar
Darmon, H. and Merel, L., Winding quotients and some variants of Fermat’s last theorem. J. reine angew. Math. 490 1997, 81–100.Google Scholar
Erdős, P. and Selfridge, J. L., The product of consecutive integers is never a power. Illinois J. Math. 19 1975, 292–301.Google Scholar
Győry, K., Hajdu, L. and Pinter, Á., Perfect powers from products of consecutive terms in arithmetic progression. Compos. Math. 145 2009, 845–864.Google Scholar
Kraus, A., Majorations effectives pour laéquation de Fermat généralisée. Canad. J. Math. 49 1997, 1139–1161.CrossRefGoogle Scholar
Lakhal, M. and Sander, J. W., Rational points on the superelliptic Erdős–Selfridge curve of fifth degree. Mathematika 50 2003, 113–124.Google Scholar
Ribet, K., On the equation a p + 2𝛼 b p + c p = 0. Acta Arith. 79 1997, 7–16.Google Scholar
Sander, J. W., Rational points on a class of superelliptic curves. J. Lond. Math. Soc. (2) 59 1999, 422–434.Google Scholar
Saradha, N. and Shorey, T. N., Almost perfect powers in arithmetic progression. Acta Arith. 99 2001, 363–388.Google Scholar
Saradha, N. and Shorey, T. N., Almost squares and factorisation in consecutive integers. Compos. Math. 138(1) 2003, 113–124.Google Scholar
Saradha, N. and Shorey, T. N., On the equation n (n + d)⋯(n + (i 0 - 1d)(n + (i 0 + 1)d)⋯(n + (k - 1)d) = y ℓ with 0 < i 0 < k - 1. Acta Arith. 129 2007, 1–21.CrossRefGoogle Scholar
Shen, Z. and Cai, T., Rational points on three superelliptic curves. Bull. Aust. Math. Soc. 85(1) 2012, 105–113.Google Scholar
Shorey, T. N., Exponential diophantine equations involving products of consecutive integers and related equations. In Number Theory (ed. Bambah, R. P. et al. ), Hindustan Book Agency (New Delhi, 1999), 463–495.Google Scholar
Shorey, T. N., Powers in arithmetic progression. In A Panaroma in Number Theory or The view from Baker’s Garden (ed. Wüstholz, G.), Cambridge University Press (Cambridge, 2002), 341–353.Google Scholar
Wiles, A., Modular elliptic curves and Fermat’s Last Theorem. Ann of Math. (2) 141 1995, 443–551.Google Scholar