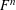Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-24T06:27:20.224Z Has data issue: false hasContentIssue false
  • English
  • Français

UNIONS OF LINES IN $F^{n}$

Part of: Harmonic analysis in several variables Discrete geometry

Published online by Cambridge University Press:  11 April 2016

Richard Oberlin
Richard Oberlin*
Affiliation:
Department of Mathematics, Florida State University, 208 Love Building, 1017 Academic way, Tallahassee, FL 32306, U.S.A. email [email protected]
Get access

Abstract

We show that if a collection of lines in a vector space over a finite field has “dimension” at least 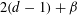$2(d-1)+\unicode[STIX]{x1D6FD}$ , then its union has “dimension” at least 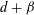$d+\unicode[STIX]{x1D6FD}$ . This is the sharp estimate of its type when no structural assumptions are placed on the collection of lines. We also consider some refinements and extensions of the main result, including estimates for unions of 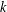$k$ -planes.

MSC classification

Primary: 42B25: Maximal functions, Littlewood-Paley theory 52C17: Packing and covering in $n$ dimensions
Type
Research Article
Information
Mathematika , Volume 62 , Issue 3 , 2016 , pp. 738 - 752
Copyright
Copyright © University College London 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bourgain, J., Katz, N. and Tao, T., A sum-product estimate in finite fields, and applications. Geom. Funct. Anal. 14(1) 2004, 27–57; MR 2053599 (2005d:11028).CrossRefGoogle Scholar
Bueti, J., An incidence bound for $k$ -planes in $F^{n}$ and a planar variant of the Kakeya maximal function. Preprint, 2006, arXiv:math/0609337 [math.CO].Google Scholar
Christ, M., Quasi extremals for a radon-like transform. Preprint, http://math.berkeley.edy/∼mchrist/Papers/quasiextremal.pdf .Google Scholar
Dvir, Z., On the size of Kakeya sets in finite fields. J. Amer. Math. Soc. 22(4) 2009, 1093–1097.CrossRefGoogle Scholar
Ellenberg, J. S., Oberlin, R. and Tao, T., The Kakeya set and maximal conjectures for algebraic varieties over finite fields. Mathematika 56(1) 2010, 1–25; MR 2604979.CrossRefGoogle Scholar
Mockenhaupt, G. and Tao, T., Restriction and Kakeya phenomena for finite fields. Duke Math. J. 121(1) 2004, 35–74; MR 2031165 (2004m:11200).CrossRefGoogle Scholar
Oberlin, D. M., Personal communication.Google Scholar
Oberlin, D. M., Unions of hyperplanes, unions of spheres, and some related estimates. Illinois J. Math. 51(4) 2007, 1265–1274; MR 2417426 (2009f:28005).CrossRefGoogle Scholar
Wolff, T., An improved bound for Kakeya type maximal functions. Rev. Mat. Iberoam. 11(3) 1995, 651–674; MR 1363209 (96m:42034).CrossRefGoogle Scholar
Wolff, T., Recent work connected with the Kakeya problem. In Prospects in Mathematics (Princeton, NJ, 1996), American Mathematical Society (Providence, RI, 1999), 129–162; MR 1660476 (2000d:42010).Google Scholar