Hostname: page-component-6bf8c574d5-w79xw Total loading time: 0 Render date: 2025-02-17T18:23:17.071Z Has data issue: false hasContentIssue false
  • English
  • Français

TRANSCENDENTAL SUMS RELATED TO THE ZEROS OF ZETA FUNCTIONS

Part of: Zeta and $L$-functions: analytic theory Diophantine approximation, transcendental number theory

Published online by Cambridge University Press:  01 August 2018

Sanoli Gun ,
M. Ram Murty  and
Purusottam Rath
Sanoli Gun
Affiliation:
Institute of Mathematical Sciences, Homi Bhabha National Institute, C.I.T Campus, Taramani, Chennai 600 113, India email [email protected]
M. Ram Murty
Affiliation:
Department of Mathematics, Queen’s University, Jeffrey Hall, 99 University Avenue, Kingston, ON K7L3N6, Canada email [email protected]
Purusottam Rath
Affiliation:
Chennai Mathematical Institute, Plot No H1, SIPCOT IT Park, Padur PO, Siruseri 603103, Tamil Nadu, India email [email protected]
Get access

Abstract

While the distribution of the non-trivial zeros of the Riemann zeta function constitutes a central theme in Mathematics, nothing is known about the algebraic nature of these non-trivial zeros. In this article, we study the transcendental nature of sums of the form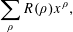

$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D70C}}R(\unicode[STIX]{x1D70C})x^{\unicode[STIX]{x1D70C}},\end{eqnarray}$$
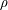where the sum is over the non-trivial zeros $\unicode[STIX]{x1D70C}$ of $\unicode[STIX]{x1D701}(s)$, 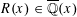$R(x)\in \overline{\mathbb{Q}}(x)$ is a rational function over algebraic numbers and 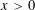$x>0$ is a real algebraic number. In particular, we show that the function
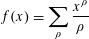$$\begin{eqnarray}f(x)=\mathop{\sum }_{\unicode[STIX]{x1D70C}}\frac{x^{\unicode[STIX]{x1D70C}}}{\unicode[STIX]{x1D70C}}\end{eqnarray}$$
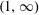 has infinitely many zeros in $(1,\infty )$, at most one of which is algebraic. The transcendence tools required for studying 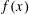$f(x)$ in the range 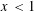$x<1$ seem to be different from those in the range 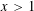$x>1$. For 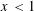$x<1$, we have the following non-vanishing theorem: If for an integer 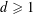$d\geqslant 1$, 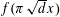$f(\unicode[STIX]{x1D70B}\sqrt{d}x)$ has a rational zero in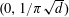$(0,1/\unicode[STIX]{x1D70B}\sqrt{d})$, then
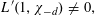$$\begin{eqnarray}L^{\prime }(1,\unicode[STIX]{x1D712}_{-d})\neq 0,\end{eqnarray}$$
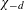 where $\unicode[STIX]{x1D712}_{-d}$ is the quadratic character associated with the imaginary quadratic field 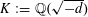$K:=\mathbb{Q}(\sqrt{-d})$. Finally, we consider analogous questions for elements in the Selberg class. Our proofs rest on results from analytic as well as transcendental number theory.

MSC classification

Primary: 11J81: Transcendence (general theory) 11J86: Linear forms in logarithms; Baker's method
Secondary: 11M06: $zeta (s)$ and $L(s, chi)$
Type
Research Article
Information
Mathematika , Volume 64 , Issue 3 , 2018 , pp. 875 - 897
Copyright
Copyright © University College London 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research of the second author was supported by an NSERC Discovery grant and a Simons Fellowship.

References

Bombieri, E. and Lagarias, J., Complements to Li’s criterion for the Riemann hypothesis. J. Number Theory 77 1999, 274–287.Google Scholar
Brown, F., Li’s criterion and zero-free regions of L-functions. J. Number Theory 111(1) 2005, 1–32.Google Scholar
Coffey, M. W., Toward verification of the Riemann hypothesis: application of the Li criterion. Math. Phys. Anal. Geom. 8 2005, 211–255.Google Scholar
Coffey, M. W., The Stieltjes constants, their relation the 𝜂 j coefficients and representation of the Hurwitz zeta function. Analysis 30 2010, 383–409.Google Scholar
Droll, A., Variations of Li’s criterion for an extension of the Selberg class. PhD Thesis, Queen’s University, Kingston, Ontario, Canada, 2012.Google Scholar
Feldman, N. and Nesterenko, Yu., Number Theory, IV, Transcendental Numbers (Encyclopaedia of Mathematical Sciences 44 ), Springer (Berlin, 1998).Google Scholar
Gross, B. H., On an identity of Chowla and Selberg. J. Number Theory 11 1979, 344–348.Google Scholar
Gun, S., Ram Murty, M. and Rath, P., Transcendence of the log gamma function and some discrete periods. J. Number Theory 129(9) 2009, 2154–2165.Google Scholar
Ingham, A. E., On two conjectures in the theory of numbers. Amer. J. Math. 64(1) 1942, 313–319.Google Scholar
Ingham, A., The Distribution of Prime Numbers (Cambridge Mathematical Library), Cambridge University Press (Cambridge, 1990); with a foreword by R. C. Vaughan.Google Scholar
Kaczorowski, J. and Perelli, A., On the structure of the Selberg class, VII: 1 < d < 2. Ann. of Math. (2) 173 2011, 1397–1441.Google Scholar
Li, X.-J., The positivity of a sequence of numbers and the Riemann hypothesis. J. Number Theory 65 1997, 325–333.Google Scholar
Ram Murty, M., Selberg conjectures and Artin L-functions. Bull. Amer. Math. Soc. 31 1994, 1–14.Google Scholar
Ram Murty, M. and Kumar Murty, V., Transcendental values of class group L-functions. Math. Ann. 351(4) 2011, 835–855.Google Scholar
Ram Murty, M. and Perelli, A., The pair correlation of zeros of functions in the Selberg class. Int. Math. Res. Not. IMRN 10 1999, 531–545.Google Scholar
Rubinstein, M. and Sarnak, P., Chebyshev’s bias. Exp. Math. 3(3) 1994, 173–197.Google Scholar
Nesterenko, Y. V., Modular functions and transcendence. Math. Sb. 187(9) 1996, 65–96.Google Scholar
Nesterenko, Y. V. and Philippon, P. (eds), Introduction to Algebraic Independence Theory (Lecture Notes in Mathematics 1752 ), Springer (Berlin, 2001).Google Scholar
Ramaré, O., Explicit estimates for the summatory function 𝛬(n)/n from the one of 𝛬(n). Acta Arith. 159 2013, 113–122.Google Scholar
Selberg, A., Old and new conjectures and results about a class of Dirichlet series. In Proceedings of the Amalfi Conference on Analytic Number Theory (Maiori, 1989), University of Salerno (Salerno, 1992), 367–385.Google Scholar
Voronin, S. M., The differential independence of 𝜁-functions. Dokl. Akad. Nauk SSSR 209 1973, 1264–1266.Google Scholar