Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T07:05:37.750Z Has data issue: false hasContentIssue false
  • English
  • Français

Transcendental numbers arising from Drinfeld modules

Published online by Cambridge University Press:  26 February 2010

Jing Yu
Jing Yu
Affiliation:
Institute of Mathematics, Academia Sinica, Taipei, Taiwan, R.O.C.
Get access

Extract

Let 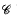be a smooth projective, geometrically irreducible curve over a finite field 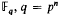. We fix a rational point ∞on 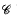, and consider the ring A of functions on 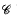regular away from ∞. We set k to be the function field of 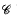and k∞ its completion at ∞. After taking algebraic closure we obtain the field 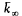whose elements will be called “numbers”.

Type
Research Article
Information
Mathematika , Volume 30 , Issue 1 , June 1983 , pp. 61 - 66
Copyright
Copyright © University College London 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

C.Carlitz, L.. On certain functions connected with polynomials in a Galois field. Duke Math. J., 1 (1935), 137–168.CrossRefGoogle Scholar
D.Drinfeld, V. G.. Elliptic Modules (Russian). Math. Sbornik, 94 (1974), 594–627 (English translation, Math. USSR Sbornik, 23 (1974), No. 4.).Google Scholar
G.Goss, D.. Von Staudt for F,[T]. Duke Math. J., 45 (1978), 885–910.CrossRefGoogle Scholar
S.Siegel, C. L.. Transcendental numbers, Annals of Math. Studies, 16 (Princeton, 1949).Google Scholar
W.Wade, L. I.. Certain quantities transcendental over GF (pn, X). Duke Math. J., 8 (1941), 701–720.CrossRefGoogle Scholar
Y.Yu, Jing. Irrationality of lattices in finite characteristic. Mathematika, 29 (1982), 227–230.CrossRefGoogle Scholar