Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T06:54:41.299Z Has data issue: false hasContentIssue false
  • English
  • Français

Totally ordered measure spaces and their Lp algebras

Part of: Set functions and measures on spaces with additional structure

Published online by Cambridge University Press:  26 February 2010

J. W. Baker ,
J. S. Pym  and
H. L. Vasudeva
J. W. Baker
Affiliation:
Department of Mathematics, University of Sheffield, Sheffield. S3 7RH
J. S. Pym
Affiliation:
Department of Mathematics, University of Sheffield, Sheffield. S3 7RH
H. L. Vasudeva
Affiliation:
Department of Mathematics, Punjab University, Chandigarh, India 160014.
Get access

Extract

This paper is concerned with two aspects of the theory of measures on compact totally ordered spaces (the topology is to be the order topology). In Section 2, we clarify a recent construction of Sapounakis [11, 12] and, in so doing, we are able to say a little more about it. It should be added here that Sapounakis had other ends in view. To be precise, let I be the closed unit interval [0, 1] and let λ be Lebesgue measure on I. We shall construct another totally ordered set Ĩ which is compact in its order topology, a continuous increasing surjection τ : Ĩ → I with the property that card τ−1(t) = 2 for all t ∈ ]0,1[ (these brackets denote the open interval), and a measure 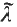on Ĩ such that τ(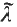) = λ. Then the following theorem holds.

MSC classification

Secondary: 28C99: None of the above, but in this section
Type
Research Article
Information
Mathematika , Volume 29 , Issue 1 , June 1982 , pp. 42 - 54
Copyright
Copyright © University College London 1982

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Baker, J. W. and Milnes, P.. The ideal structure of the Stone-Čech compactiflcation of a group. Math. Proc. Cambridge Phil. Soc., 82 (1977), 401–409.CrossRefGoogle Scholar
2.Bonsall, F. F. and Duncan, J.. Complete normed algebras (Springer, Berlin, 1973).CrossRefGoogle Scholar
3.Dhar, R. K. and Vasudeva, H. L.. L1 (I, X) with order convolution. Proc. Amer. Math. Soc, to appear.Google Scholar
4.Duchon, M.. Structure theory for a class of convolution algebras of vector valued measures. Math. Nachr., 60 (1974), 97–108.CrossRefGoogle Scholar
5.Dunford, N. and Schwartz, J. T.. Linear Operators, Part I (Interscience, New York, 1957).Google Scholar
6.Ellis, R.. Lectures on topological dynamics (Benjamin, New York, 1969).Google Scholar
7.Hewitt, E. and Zuckermann, H. S.. Structure theory for a class of convolution algebras. Pacific J. Math., 7 (1957), 913–941.CrossRefGoogle Scholar
8.Larsen, R.. An introduction to the theory of multipliers (Springer, Berlin, 1971).CrossRefGoogle Scholar
9.Larsen, R.. The multipliers of L1([0,1]) with order convolution. Publ. Math. Debrecen, 23 (1976), 239–248.CrossRefGoogle Scholar
10.Ross, K. A.. The structure of certain measure algebras. Pacific J. Math., 11 (1961), 723–737.CrossRefGoogle Scholar
11.Sapounakis, A.. Properties of measures on topological spaces, Thesis (University of Liverpool, 1980).Google Scholar
12.Sapounakis, A.. Measures on totally ordered spaces. Mathematika, 27 (1980), 225–235.CrossRefGoogle Scholar
13.Todd, D. G.. Multipliers of certain convolution algebras over locally compact semigroups. Math. Proc. Cambridge Phil. Soc., 87 (1980), 51–59.CrossRefGoogle Scholar
14.Zelazko, W.. On the algebras Lp of locally compact groups. Colloq. Math., 8 (1961), 115–120.CrossRefGoogle Scholar