Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Zong, Chuanming
2014.
Packing, covering and tiling in two-dimensional spaces.
Expositiones Mathematicae,
Vol. 32,
Issue. 4,
p.
297.
Bhattacharya, Amitava
and
Mondal, Anupam
2020.
Covering the plane by a sequence of circular disks with a constraint.
Computational Geometry,
Vol. 91,
Issue. ,
p.
101680.


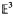 with certain congruent ellipsoids.
with certain congruent ellipsoids.