Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T05:35:23.283Z Has data issue: false hasContentIssue false
  • English
  • Français

A theorem on the existence of non-σ-finite subsets

Published online by Cambridge University Press:  26 February 2010

Roy O. Davies
Roy O. Davies
Affiliation:
The University, Leicester
Get access

Extract

Let Ω be a compact metric space of non-σ-finite Λh-measure, where Λh denotes the Hausdorff measure corresponding to some continuous increasing real function h(t), denned for t ≥ 0 and with h(t) > 0 and h(t) > 0 for t > 0. C. A. Rogers has drawn attention to two problems that have remained unsolved for some years, and which seem to present considerable difficulty:

I. Does Ω necessarily have subsets of finite positive Λh-measure?

II. Does Ω. necessarily contain a system of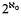disjoint closed subsets each of non-σ-finite Λh-measure ?

The answers are affirmative when Ω is a subset of a Euclidean space (see [1], [2], [3], [4], [5]); recently D. G. Larman ([8], [9]) was able to extend each of these results to the case of the “finite-dimensional” compact metric spaces that he introduced in [7]. Both of his proofs depend on the detailed structure of such spaces; the aim of the present paper is to establish a general theorem, from which it follows in particular that Larman's second result is a consequence of his first, and that an affirmative answer to I would imply an affirmative answer to II. (Since it seems likely that I must be answered negatively in general, and II affirmatively, the present theorem may well be of only ephemeral significance; the nature of the proof reinforces this expectation.)

Type
Research Article
Information
Mathematika , Volume 15 , Issue 1 , June 1968 , pp. 60 - 62
Copyright
Copyright © University College London 1968

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Besicovitch, A. S., “A theorem on s-dimensional measure of sets of points”, Proc. Cambridge Phil. Soc, 38 (1942), 24–27.Google Scholar
2.Besicovitch, A. S., “On the existence of subsets of finite measure of sets of infinite measure”, Indag. Math., 14 (1952), 339–344.Google Scholar
3.Besicovitch, A. S., “On the definition of tangents to sets of infinite linear measure”, Proc. Cambridge Phil. Soc., 52 (1956), 20–29.CrossRefGoogle Scholar
4.Davies, Roy O., “Subsets of finite measure in analytic sets”, Indag. Math., 14 (1952), 488–489.CrossRefGoogle Scholar
5.Davies, Roy O., “Non-σ-finite closed subsets of analytic sets”, Proc. Cambridge Phil. Soc., 52 (1956), 174–177.CrossRefGoogle Scholar
6.Kuratowski, C., Topologie, Vol. I, 4th ed.; Vol. II, 3rd ed. (Warsaw, 1958 and 1961).Google Scholar
7.Larman, D. G., “A new theory of dimension”, Proc. London Math. Soc. (3), 17 (1967), 168–192.Google Scholar
8.Larman, D. G., “On Hausdorff measure in finite-dimensional compact metric spaces”, Proc. London Math. Soc. (3), 17 (1967), 193–206.CrossRefGoogle Scholar
9.Larman, D. G., “On selection of non-σ-finite subsets”, Mathematika, 14 (1967), 161–164.CrossRefGoogle Scholar
10.Sion, M. and Sjerve, D., “Approximation properties of measures generated by continuous set functions”, Mathematika, 9 (1962), 145–156.CrossRefGoogle Scholar