Hostname: page-component-5cf477f64f-2wr7h Total loading time: 0 Render date: 2025-04-04T22:52:27.820Z Has data issue: false hasContentIssue false
  • English
  • Français

TERNARY DIVISOR FUNCTIONS IN ARITHMETIC PROGRESSIONS TO SMOOTH MODULI

Part of: Multiplicative number theory Sequences and sets Finite fields and commutative rings (number-theoretic aspects) Exponential sums and character sums

Published online by Cambridge University Press:  19 June 2018

Ping Xi
Ping Xi*
Affiliation:
School of Mathematics and Statistics, Xi’an Jiaotong University, Xi’an 710049, P.R. China email [email protected]
Get access

Abstract

We prove that the exponent of distribution of 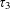$\unicode[STIX]{x1D70F}_{3}$ in arithmetic progressions can be as large as 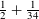$\frac{1}{2}+\frac{1}{34}$, provided that the moduli is squarefree and has only sufficiently small prime factors. The tools involve arithmetic exponent pairs for algebraic trace functions, as well as a double 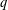$q$-analogue of the van der Corput method for smooth bilinear forms.

MSC classification

Primary: 11N37: Asymptotic results on arithmetic functions 11N25: Distribution of integers with specified multiplicative constraints 11B25: Arithmetic progressions 11T23: Exponential sums 11L05: Gauss and Kloosterman sums; generalizations
Type
Research Article
Information
Mathematika , Volume 64 , Issue 3 , 2018 , pp. 701 - 729
Copyright
Copyright © University College London 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andersson, J., Summation formulae and zeta functions, Doctoral Dissertation, Stockholm University, 2006.Google Scholar
Deligne, P., La conjecture de Weil, II. Publ. Math. Inst. Hautes Études Sci. 52 1980, 137–252.Google Scholar
Fouvry, É., Sur le problème des diviseurs de Titchmarsh. J. Reine Angew. Math. 357 1985, 51–76.Google Scholar
Fouvry, É., Kowalski, E. and Michel, Ph., On the conductor of cohomological transforms. Preprint, 2013, arXiv:1310.3603 [math.NT].Google Scholar
Fouvry, É., Kowalski, E. and Michel, Ph., Algebraic trace functions over the primes. Duke Math. J. 163 2014, 1683–1736.Google Scholar
Fouvry, É., Kowalski, E. and Michel, Ph., On the exponent of distribution of the ternary divisor function. Mathematika 61 2015, 121–144.Google Scholar
Fouvry, É., Kowalski, E. and Michel, Ph., Algebraic twists of modular forms and Hecke orbits. Geom. Funct. Anal. 25 2015, 580–657.Google Scholar
Fouvry, É., Kowalski, E. and Michel, Ph., Trace functions over finite fields and their applications. In Colloquium de Giorgi, 2013 and 2014, Scuola Normale Superiore Pisa (2015), 7–35.Google Scholar
Friedlander, J. B. and Iwaniec, H., Incomplete Kloosterman sums and a divisor problem (with an appendix by B. J. Birch and E. Bombieri). Ann. of Math. (2) 121 1985, 319–350.Google Scholar
Graham, S. W. and Kolesnik, G., Van der Corput Method of Exponential Sums (London Mathematical Society Lecture Note Series 126 ), Cambridge University Press (Cambridge, 1991).Google Scholar
Heath-Brown, D. R., The divisor function d 3(n) in arithmetic progressions. Acta Arith. 47 1986, 29–56.Google Scholar
Hooley, C., An asymptotic formula in the theory of numbers. Proc. Lond. Math. Soc. (3) 7 1957, 396–413.Google Scholar
Irving, A. J., The divisor function in arithmetic progressions to smooth moduli. Int. Math. Res. Not. IMRN 15 2015, 6675–6698.Google Scholar
Katz, N. M., Exponential Sums and Differential Equations (Annals of Math. Studies 124 ), Princeton University Press (1990).Google Scholar
Kuznetsov, N. V., The Petersson conjecture for cusp forms of weight zero and the Linnik conjecture. Sums of Kloosterman sums. Mat. Sb. 111(153) 1980, 334–383; 479.Google Scholar
Linnik, Yu. V., All large numbers are sums of a prime and two squares (A problem of Hardy and Littlewood). II. Mat. Sb. 53(95) 1961, 3–38.Google Scholar
Matthes, R., An elementary proof of a formula of Kuznecov for Kloosterman sums. Results Math. 18 1990, 120–124.Google Scholar
Polymath, D. H. L., New equidistribution estimates of Zhang type. Algebra Number Theory 8 2014, 2067–2199.Google Scholar
Selberg, A., Lectures on Sieves (Collected Papers II ), Springer (1991), 65–247.Google Scholar
Smith, R. A., On n-dimensional Kloosterman sums. J. Number Theory 11 1979, 324–343.Google Scholar
Smith, R. A., A generalization of Kuznietsov’s identity for Kloosterman sums. C. R. Math. Rep. Acad. Sci. Canada 2(6) 1980, 315–320.Google Scholar
Wu, J. and Xi, P., Arithmetic exponent pairs for algebraic trace functions and applications. Preprint, 2016, arXiv:1603.07060 [math.NT].Google Scholar