Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T05:45:32.588Z Has data issue: false hasContentIssue false
  • English
  • Français

SUBGROUPS OF FRACTIONAL DIMENSION IN NILPOTENT OR SOLVABLE LIE GROUPS

Part of: Lie groups Classical measure theory

Published online by Cambridge University Press:  23 May 2013

Nicolas de Saxcé
Nicolas de Saxcé*
Affiliation:
Institute of Mathematics, Hebrew University, 91904 Jerusalem,Israel email [email protected]
Get access

Abstract

We construct dense Borel measurable subgroups of Lie groups of intermediate Hausdorff dimension. In particular, we generalize the Erdős–Volkmann construction [Additive Gruppen mit vorgegebener Hausdorffscher Dimension, J. Reine Angew. Math. 221 (1966), 203–208], showing that any nilpotent 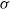$\sigma $-compact Lie group 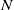$N$ admits dense Borel subgroups of arbitrary dimension between zero and 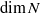$\dim N$. In algebraic groups defined over a finite extension of the rationals, using diophantine properties of algebraic numbers, we are also able to construct dense subgroups of arbitrary dimension, but the general case remains open. In particular, we raise the following question: does there exist a measurable proper subgroup of 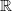$ \mathbb{R} $ of positive Hausdorff dimension which is stable under multiplication by a transcendental number? Subgroups of nilpotent 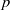$p$-adic analytic groups are also discussed.

MSC classification

Secondary: 22E25: Nilpotent and solvable Lie groups 28A78: Hausdorff and packing measures
Type
Research Article
Information
Mathematika , Volume 59 , Issue 2 , July 2013 , pp. 497 - 511
Copyright
Copyright © University College London 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abercrombie, A. G., Subgroups and subrings of profinite rings. Math. Proc. Cambridge Philos. Soc. 116 (1994), 209–222.CrossRefGoogle Scholar
Borel, A., Linear Algebraic Groups, 2nd edn. (Graduate Texts in Mathematics 126), Springer (New York, NY, 1991).CrossRefGoogle Scholar
Breuillard, E., Green, B. J. and Tao, T., Approximate subgroups of linear groups. Geom. Funct. Anal. 21 (2011), 774–819.CrossRefGoogle Scholar
Breuillard, E., Green, B. J. and Tao, T., The structure of approximate subgroups. Publ. Math. Inst. Hautes Études Sci. 116 (2012), 115–221.CrossRefGoogle Scholar
Corwin, L. and Greenleaf, F. P., Representations of Nilpotent Lie Groups and their Applications, Part I, Basic Theory and Examples, Cambridge University Press (1990).Google Scholar
Erdős, P. and Volkmann, K. J., Additive Gruppen mit vorgegebener Hausdorffscher Dimension. J. Reine Angew. Math. 221 (1966), 203–208.Google Scholar
Falconer, K. J., Fractal Geometry, 2nd edn. (Mathematical foundations and applications), John Wiley & Sons (Hoboken, NJ, 2003).CrossRefGoogle Scholar
Platonov, V. and Rapinchuk, A, Algebraic Groups and Number Theory (Pure and Applied Mathematics 139), Academic Press (Boston, MA, 1994).Google Scholar
Raghunathan, M. S., Discrete Subgroups of Lie Groups (Ergebnisse der Mathematik und ihrer Grenzgebiete 68), Springer (1972).CrossRefGoogle Scholar
de Saxcé, N., Sous-groupes boréliens des groupes de Lie. Doctoral Thesis, Université Paris Sud (11), 2012.Google Scholar
de Saxcé, N., Trou dimensionnel dans les groupes de Lie simples compacts via les séries de Fourier. J. Anal. Math. (to appear).Google Scholar
Serre, J.-P., Lie Algebras and Lie groups: 1964 Lectures given at Harvard University, 2nd edn. (Lecture Notes in Mathematics 1500), Springer (Berlin, 1992).CrossRefGoogle Scholar