Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Sjölin, Per
1993.
Estimates of spherial averages of Fourier transforms and dimensions of sets.
Mathematika,
Vol. 40,
Issue. 2,
p.
322.
Bourgain, Jean
1994.
Hausdorff dimension and distance sets.
Israel Journal of Mathematics,
Vol. 87,
Issue. 1-3,
p.
193.
Mitsis, Themis
2001.
A note on the distance set problem in the plane.
Proceedings of the American Mathematical Society,
Vol. 130,
Issue. 6,
p.
1669.
Muravnik, A.B.
2001.
Recent Progress in Functional Analysis, Proceedings of the International Functional Analysis Meeting on the Occasion of the 70th Birthday of Professor Manuel Valdivia.
Vol. 189,
Issue. ,
p.
335.
Hare, Kathryn
and
Roginskaya, Maria
2003.
The energy of signed measures.
Proceedings of the American Mathematical Society,
Vol. 132,
Issue. 2,
p.
397.
Hare, Kathryn E.
and
Roginskaya, Maria
2003.
Multipliers of spherical harmonics and energy of measures on the sphere.
Arkiv för Matematik,
Vol. 41,
Issue. 2,
p.
281.
Hofmann, S.
and
Iosevich, A.
2004.
Circular averages and Falconer/Erdös distance conjecture in the plane for random metrics.
Proceedings of the American Mathematical Society,
Vol. 133,
Issue. 1,
p.
133.
Iosevich, A.
and
Rudnev, M.
2007.
Erdös distance problem in vector spaces over finite fields.
Transactions of the American Mathematical Society,
Vol. 359,
Issue. 12,
p.
6127.
IOSEVICH, A.
and
RUDNEV, M.
2009.
FREIMAN THEOREM, FOURIER TRANSFORM AND ADDITIVE STRUCTURE OF MEASURES.
Journal of the Australian Mathematical Society,
Vol. 86,
Issue. 1,
p.
97.
Alexandrov, Alexey
and
Rozenblum, Grigori
2009.
Finite rank Toeplitz operators: Some extensions of D. Luecking's theorem.
Journal of Functional Analysis,
Vol. 256,
Issue. 7,
p.
2291.
Shayya, Bassam
2011.
Measures with Fourier Transforms in L2 of a Half-space.
Canadian Mathematical Bulletin,
Vol. 54,
Issue. 1,
p.
172.
Barceló, Juan Antonio
Bennett, Jonathan
Carbery, Anthony
and
Rogers, Keith M.
2011.
On the dimension of divergence sets of dispersive equations.
Mathematische Annalen,
Vol. 349,
Issue. 3,
p.
599.
Eswarathasan, Suresh
Iosevich, Alex
and
Taylor, Krystal
2011.
Fourier integral operators, fractal sets, and the regular value theorem.
Advances in Mathematics,
Vol. 228,
Issue. 4,
p.
2385.
Greenleaf, Allan
and
Iosevich, Alex
2012.
On triangles determined by subsets of the Euclidean plane, the associated bilinear operators and applications to discrete geometry.
Analysis & PDE,
Vol. 5,
Issue. 2,
p.
397.
Iosevich, Alex
Mourgoglou, Mihalis
and
Senger, Steven
2012.
On sets of directions determined by subsets of ℝ d.
Journal d'Analyse Mathématique,
Vol. 116,
Issue. 1,
p.
355.
Koh, Doowon
and
Shen, Chun-Yen
2012.
The generalized Erdős–Falconer distance problems in vector spaces over finite fields.
Journal of Number Theory,
Vol. 132,
Issue. 11,
p.
2455.
Koh, Doowon
and
Pi, Youngjin
2013.
SIZE OF DOT PRODUCT SETS DETERMINED BY PAIRS OF SUBSETS OF VECTOR SPACES OVER FINITE FIELDS.
Journal of the Chungcheong Mathematical Society,
Vol. 26,
Issue. 4,
p.
853.
Iosevich, Alex
and
Senger, Steven
2014.
Combinatorial and Additive Number Theory.
Vol. 101,
Issue. ,
p.
63.
Liu, Bochen
2014.
On Radii of Spheres Determined by Subsets of Euclidean Space.
Journal of Fourier Analysis and Applications,
Vol. 20,
Issue. 3,
p.
668.
Fässler, Katrin
and
Orponen, Tuomas
2014.
On restricted families of projections in ℝ3
.
Proceedings of the London Mathematical Society,
Vol. 109,
Issue. 2,
p.
353.


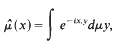
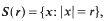
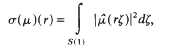
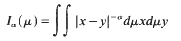
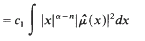
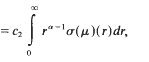
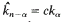 where
where  .
.