Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T04:59:48.724Z Has data issue: false hasContentIssue false
  • English
  • Français

Speciality of full subalgebras and rational identities in Jordan algebras

Part of: Jordan algebras

Published online by Cambridge University Press:  26 February 2010

H. Essannouni  and
A. Kaidi
H. Essannouni
Affiliation:
Departement de Mathématiques et d'Informatique, Faculté des Sciences, University Mohammed V, B.P. 1014. Rabat, Morocco.
A. Kaidi
Affiliation:
Departement de Mathématiques et d'Informatique, Faculté des Sciences, University Mohammed V, B.P. 1014. Rabat, Morocco.
Get access

Extract

The Shirshov-Cohn theorem asserts that in a Jordan algebra (with 1), any subalgebra generated by two elements (and 1) is special. Let J be a Jordan algebra with 1, a, b elements of J and let a1, a2, …, an be invertible elements of J such that

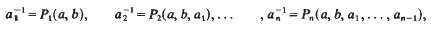
Where

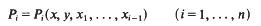
are Jordan polynomials. In [2, p. 425] Jacobson conjectured that for any choice of the Pi the subalgebra of J generated by 1, a, b, a1…, an is special.

MSC classification

Secondary: 17C05: Identities and free Jordan structures
Type
Research Article
Information
Mathematika , Volume 39 , Issue 2 , December 1992 , pp. 327 - 329
Copyright
Copyright © University College London 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Essannouni, H.Garijo, P. JiminezKaidi, A. and Palacios, A. Rodriguez. Rational identities in Jordan algebra. Algebras Groups Geom., 5 (1988), 411–420.Google Scholar
2.Jacobson, N.. Structure and representation of Jordan algebras. Amer. Math. Soc. Coll. Publ 39 (Providence, Rhode Island, 1968).Google Scholar
3.Martindale, W. S. and McCrimmon, K.. Imbedding nondegenerate Jordan algebras in semiprimitive algebras. Proc. Amer. Math. Soc., 103 (1988), 1031–1036.CrossRefGoogle Scholar
4.Moreno, J. Martinez. Sobre algebras de Jordan normadas completas. Tesis doctoral (Univ. de Granada, 1977).Google Scholar
5.McCrimmon, K.. Macdonald's theorem with inverses. Pacific J. Math., 21 (1967), 315–325.CrossRefGoogle Scholar
6.McCrimmon, J.. The radical of Jordan algebras. Proc. Nat. Acad. Sci. U.S.A., 62 (1969), 671–678.CrossRefGoogle Scholar
7.Zelmanov, E.. On prime Jordan algebras II. Siberian, Math. J., 24 (1983).Google Scholar