Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T04:57:45.467Z Has data issue: false hasContentIssue false
  • English
  • Français

The spatial distribution of algebraic integers on constant-norm hypersurfaces

Part of: Algebraic number theory: global fields

Published online by Cambridge University Press:  26 February 2010

R. W. K. Odoni
R. W. K. Odoni
Affiliation:
Department of Mathematics, University of Glasgow, Glasgow, G12 8QW, Scotland.
Get access

Abstract

Let K be an algebraic number field, [ K: 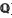] = KΣ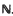. Most of what we shall discuss is trivial when K = 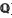, so that we assume that K ≥ 2 from now onwards. To describe our results, we consider the classical device [2] of Minkowski, whereby K is embedded (diagonally-) into the direct product MK of its completions at its (inequivalent) infinite places. Thus MK is 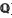-algebra isomorphic to 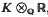, and is to be regarded as a topological 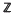-algebra, dimRMK = K, in which K is everywhere dense, while the ring Zx of integers of K embeds as a discrete 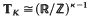-submodule of rank K. Following the ideas implicit in Hecke's fundamental papers [6] we may measure the “spatial distribution” of points of MK (modulo units of 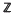κ) by means of a canonical projection onto a certain torus 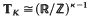. The principal application of our main results (Theorems I–III described below) is to the study of the spatial distribution of the 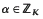which have a fixed norm n = NK/Q(α). In §2 we shall show that, with suitable interpretations, for “typical” n (for which NK/Q(α) = n is soluble), these α have “almost uniform” spatial distribution under the canonical projection onto TK. Analogous questions have been considered by several authors (see, e.g., [5, 9, 14]), but in all cases, they have considered weighted averages over such n of a type which make it impossible to make useful statements for “typical” n.

MSC classification

Secondary: 11R45: Density theorems
Type
Research Article
Information
Mathematika , Volume 39 , Issue 2 , December 1992 , pp. 350 - 366
Copyright
Copyright © University College London 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Babaev, G.. Asymptotic-geometric properties of the set of integral points on a circle and on certain ellipses (in Russian). Izv. Vyssh. Uchebn. Zaved Matematika, 31 (1962), 14–18.Google Scholar
2.Borevich, Z. I. and Shafarevich, I. R.. Number Theory (Academic Press, New York, 1966).Google Scholar
3.Cassels, J. W. S. and Frolich, A.. Algebraic Number Theory (Academic Press, New York, 1967), Ch. XV.Google Scholar
4.Draxl, P. K. J.. L-Funktionen algebraischer Tori. J. Number Theory, 3 (1971), 444–467.Google Scholar
5.Fomenko, O. M.. Extendability to the whole plane and the functional equation for the scalar product of Hecke L-series of two quadratic fields (in Russian). Proc. Steklov Inst., 128 (1972), 275–286.Google Scholar
6.Hecke, E.. Mathematische Werke (Vandenhock & Ruprecht, Göttingen, 1959), 249–289.Google Scholar
7.Kurokawa, N.. On the meromorphy of Euler products. Proc. Japan Acad., 54A (1978), 163–166.Google Scholar
8.Kurokawa, N.. On the meromorphy of Euler products I, II. Proc. London Math. Soc, 56 (1986), 1-47; 209–236.Google Scholar
9.Moroz, B. Z.. Vistas in analytic number theory. Bonner Mathematische Schriften, 156 (1984).Google Scholar
10.Narkiewicz, W.. Elementary and analytic theory of algebraic numbers, 2nd ed. (Springer, New York/PWN Warszawa 1990), Ch. 7, pp. 379–389.Google Scholar
11.Odoni, R. W. K.. Notes on the method of Frobenian functions, with applications to Fourier coefficients of modular forms. In Elementary and analytic theory of numbers, Banach Centre Publications, 17 (1985), 371–403.Google Scholar
12.Odoni, R. W. K.. On the distribution of norms of ideals in given ray-classes, and the theory of central ray-class fields. Ada Arithmetica, 52 (1989), 373–397.Google Scholar
13.Serre, J.-P.. Représentations linéaires des groupes finis (Hermann, Paris, 2ème éd., 1971).Google Scholar
14.Vinogradov, A. I.. On the extension to the left half-plane of the scalar product of Hecke's L-series “mit Grossencharakteren” (in Russian). Izv. Aka. Nauk SSSR, 29 (1965), 485–492.Google Scholar
15.Vinogradov, I. M.. The method of trigonometrical sums in the theory of numbers. English translation by Davenport, Anne and Roth, K. F. (Wiley-Interscience, New York, 1954).Google Scholar