Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-30T23:27:17.209Z Has data issue: false hasContentIssue false
  • English
  • Français

Space tiling zonotopes

Published online by Cambridge University Press:  26 February 2010

P. McMullen
P. McMullen
Affiliation:
University College London, Gower Street, London WC1E 6BT.
Get access

Abstract

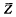A d-dimensional zonotope Z in Ed which is the vector sum of n line segments is linearly equivalent to the image of a regular n-cube under some orthogonal projection. The zonotope in En-d which is the image of the same cube under projection on to the orthogonal complementary subspace is said to be associated with Z. In this paper is proved a conjecture of G. C. Shephard, which asserts that, if Z tiles Ed by translation, with adjacent zonotopes meeting facet against facet, then 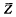tiles En-d in the same manner. A number of conditions, conjectured by Shephard and H. S. M. Coxeter to be equivalent to the tiling property, are also proved.

Type
Research Article
Information
Mathematika , Volume 22 , Issue 2 , December 1975 , pp. 202 - 211
Copyright
Copyright © University College London 1975

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Coxeter, H. S. M.. “The classification of zonohedra by means of projective diagrams”, J. Math. Pures Appi, 41 (1962), 137–156; MR25#4417.Google Scholar
McMullen, P.. “On zonotopes”, Trans. Amer. Math. Soc., 159 (1971), 91–110; MR43#5410.CrossRefGoogle Scholar
Shephard, G. C.. “Combinatorial properties of associated zonotopes”, Canad. J. Math., 26 (1974), 302–321.CrossRefGoogle Scholar
Shephard, G. C.. “Space filling zonotopes”, Mathematika, 21 (1974), 261–269.Google Scholar