Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-29T20:13:14.068Z Has data issue: false hasContentIssue false
  • English
  • Français

Some infinite families of satellite knots with given Alexander polynomial

Part of: Low-dimensional topology

Published online by Cambridge University Press:  26 February 2010

P. R. Cromwell
P. R. Cromwell
Affiliation:
Dr. P. R. Cromwell, School of Mathematics, University of Wales, Bangor, Gwynedd, LL57 1UT.
Get access

Extract

For satellite knots there is a well-known formula which relates the Alexander polynomial of the satellite to those of a companion knot and the corresponding pattern. If &s, &C and &P are the Alexander polynomials of a satellite, companion and pattern respectively then

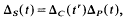
where 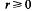is the linking number of P with a meridian of the companion torus (see [BZ], p. 118). Analogous relationships do not exist for other knot polynomials [MS]. This suggests that the existence of the above formula depends more on the geometry underlying the polynomial than on the geometry of the satellite construction.

MSC classification

Secondary: 57M25: Knots and links in $S^3$
Type
Research Article
Information
Mathematika , Volume 38 , Issue 1 , June 1991 , pp. 156 - 169
Copyright
Copyright © University College London 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bu. Burau, W.. Kennzeichnung der schlauchknoten. Abh. Math. Sem. Hamburg, 9 (1932), 125–133.Google Scholar
BZ. Burde, G. and Zieschang, H.. Knots (de Gruyter, 1985).Google Scholar
Co. Conway, J. H.. An enumeration of knots and links and some of their related properties. Computational problems in abstract algebra (1969), 329–358.Google Scholar
Cr. Cromwell, P. R.. Lonely knots and tangles: identifying knots with no companions. To appear in Mathematika.Google Scholar
J-S. Jaco, W. H. and Shalen, P. B.. Seifert fibred spaces in 3-manifolds. Memoires of the Amer. Math. Soc, 21 (1979).Google Scholar
Jo. Johannson, K.. Homotopy equivalences of 3-manifolds with boundaries. Springer Lecture Notes in Math., 761 (1979).Google Scholar
Ka. Kauffman, L. H.. The Conway polynomial. Topology, 20 (1981), 101–108.Google Scholar
Mo. Morton, H. R.. Fibred knots with a given Alexander polynomial. Venseignement Math., 31 (1983), 205–222.Google Scholar
MS. Morton, H. R. and Short, H. B.. The 2-variable polynomial of cable knots. Math. Proc. Camb. Phil. Soc, 101 (1987), 267–278.Google Scholar
Sc. Schubert, H.. Uber eine numerische Knoteninvariante. Math. Z, 61 (1954), 245–288.Google Scholar
Si. Simon, J.. An algebraic classification on knots in S3. Ann. of Math., 97 (1973), 1–13.Google Scholar
Th. Thurston, W. P.. The geometry and topology of 3-manifolds (Princeton Univ. Press, 1984).Google Scholar