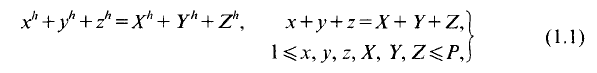Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Vaughan, R. C.
and
Wooley, T. D.
1995.
On a certain nonary cubic form and related equations.
Duke Mathematical Journal,
Vol. 80,
Issue. 3,
Parsell, Scott T.
and
Wooley, Trevor D.
2002.
A quasi-paucity problem.
Michigan Mathematical Journal,
Vol. 50,
Issue. 3,
Browning, T.D.
and
Heath-Brown, D.R.
2004.
Equal sums of three powers.
Inventiones mathematicae,
Vol. 157,
Issue. 3,
p.
553.
Blomer, V.
and
Brüdern, J.
2010.
The number of integer points on Vinogradov’s quadric.
Monatshefte für Mathematik,
Vol. 160,
Issue. 3,
p.
243.
Bourgain, Jean
and
Demeter, Ciprian
2015.
The proof of the l^2 Decoupling Conjecture.
Annals of Mathematics,
p.
351.
Brüdern, Jörg
and
Robert, Olivier
2015.
Rational points on linear slices of diagonal hypersurfaces.
Nagoya Mathematical Journal,
Vol. 218,
Issue. ,
p.
51.
Brüdern, Jörg
and
Robert, Olivier
2015.
Rational points on linear slices of diagonal hypersurfaces.
Nagoya Mathematical Journal,
Vol. 218,
Issue. ,
p.
51.
WOOLEY, TREVOR D.
2023.
Paucity problems and some relatives of Vinogradov’s mean value theorem.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 175,
Issue. 2,
p.
327.
WOOLEY, TREVOR D.
2023.
THE PAUCITY PROBLEM FOR CERTAIN SYMMETRIC DIOPHANTINE EQUATIONS.
Bulletin of the Australian Mathematical Society,
Vol. 108,
Issue. 1,
p.
29.