Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Erdös, P.
Fried, E.
Hajnal, A.
and
Milner, E. C.
1972.
Some remarks on simple tournaments.
Algebra Universalis,
Vol. 2,
Issue. 1,
p.
238.
Pouzet, M.
1985.
Graphs and Order.
p.
592.
Astie-Vidal, A.
and
Matteo, A.
1989.
Applied Algebra, Algebraic Algorithms and Error-Correcting Codes.
Vol. 356,
Issue. ,
p.
1.
Imrich, Wilfried
and
Nešetřil, Jaroslav
1992.
Simple tournaments and sharply transitive groups.
Discrete Mathematics,
Vol. 108,
Issue. 1-3,
p.
159.
Müller, Vladimír
Nešetřil, Jaroslav
and
Rödl, Vojtěch
2009.
Some recollections on early work with Jan Pelant.
Topology and its Applications,
Vol. 156,
Issue. 7,
p.
1438.
Brignall, Robert
2010.
Permutation Patterns.
p.
41.
Brignall, Robert
Ruškuc, Nik
and
Vatter, Vincent
2011.
SIMPLE EXTENSIONS OF COMBINATORIAL STRUCTURES.
Mathematika,
Vol. 57,
Issue. 2,
p.
193.
Hajnal, András
2013.
The Mathematics of Paul Erdős II.
p.
379.
Letzter, Shoham
2017.
Radon numbers for trees.
Discrete Mathematics,
Vol. 340,
Issue. 3,
p.
333.
Belkhechine, Houmem
and
Ben Salha, Cherifa
2021.
Making a Tournament Indecomposable by One Subtournament-Reversal Operation.
Graphs and Combinatorics,
Vol. 37,
Issue. 3,
p.
823.
Belkhechine, Houmem
Ben Salha, Cherifa
and
Romdhane, Rim
2024.
Irreducible Pairings and Indecomposable Tournaments.
Graphs and Combinatorics,
Vol. 40,
Issue. 4,
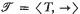 is a relational structure on the non-empty set T such that for x, y ∈ T exactly one of the three relations
is a relational structure on the non-empty set T such that for x, y ∈ T exactly one of the three relations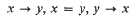
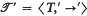 is a subtournament of
is a subtournament of 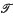 , and
, and 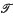 is an extension of
is an extension of 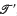 , if T′ ⊂ T and →′ is the restriction of → to T′; we will usually write 〈′, → 〉 instead of 〈 ′, → ′〉. In particular, if |T − T′| = k, we call
, if T′ ⊂ T and →′ is the restriction of → to T′; we will usually write 〈′, → 〉 instead of 〈 ′, → ′〉. In particular, if |T − T′| = k, we call 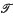 a k-poinf extension of
a k-poinf extension of 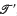 .
.