Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-20T16:19:57.522Z Has data issue: false hasContentIssue false
  • English
  • Français

SHIFTED MOMENTS OF 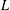$L$-FUNCTIONS AND MOMENTS OF THETA FUNCTIONS

Part of: Exponential sums and character sums Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  27 September 2016

Marc Munsch
Marc Munsch*
Affiliation:
5010 Institut für Analysis und Zahlentheorie, Steyrergasse 30, 8010 Graz, Austria email [email protected]
Get access

Abstract

Assuming the Riemann Hypothesis, Soundararajan [Ann. of Math. (2) 170 (2009), 981–993] showed that 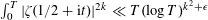$\int _{0}^{T}|\unicode[STIX]{x1D701}(1/2+\text{i}t)|^{2k}\ll T(\log T)^{k^{2}+\unicode[STIX]{x1D716}}$. His method was used by Chandee [Q. J. Math.62 (2011), 545–572] to obtain upper bounds for shifted moments of the Riemann Zeta function. Building on these ideas of Chandee and Soundararajan, we obtain, conditionally, upper bounds for shifted moments of Dirichlet 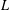$L$-functions which allow us to derive upper bounds for moments of theta functions.

MSC classification

Primary: 11M06: $zeta (s)$ and $L(s, chi)$ 11M26: Nonreal zeros of $zeta (s)$ and $L(s, chi)$; Riemann and other hypotheses
Secondary: 11L20: Sums over primes
Type
Research Article
Information
Mathematika , Volume 63 , Issue 1 , 2017 , pp. 196 - 212
Copyright
Copyright © University College London 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Chandee, V., Explicit upper bounds for L-functions on the critical line. Proc. Amer. Math. Soc. 137 2009, 4049–4063.CrossRefGoogle Scholar
Chandee, V. and Li, X., The eighth moment of Dirichlet L-functions. Adv. Math. 259 2014, 339–375.CrossRefGoogle Scholar
Chandee, V., On the correlation of shifted values of the Riemann zeta function. Q. J. Math. 62 2011, 545–572.CrossRefGoogle Scholar
Chandee, V. and Soundararajan, K., Bounding |𝜁(1/2 + it)| on the Riemann hypothesis. Bull. Lond. Math. Soc. (2) 43 2011, 243–250.CrossRefGoogle Scholar
Cohen, H. and Zagier, D., Vanishing and non-vanishing theta values. Ann. Math. Québec 37 2013, 45–61.CrossRefGoogle Scholar
Conrey, J. B. and Farmer, D. W., Mean values of L-functions and symmetry. Int. Math. Res. Not. IMRN 17 2000, 883–908.CrossRefGoogle Scholar
Conrey, J. B., Farmer, D. W., Keating, J. P., Rubinstein, M. O. and Snaith, N. C., Integral moments of L-functions. Proc. Lond. Math. Soc. (3) 91 2005, 33–104.CrossRefGoogle Scholar
Davenport, H., Multiplicative Number Theory (Graduate Texts in Mathematics 74 ), Springer (2000).Google Scholar
Granville, A. and Soundararajan, K., Multiplicative number theory: The pretentious approach. Course notes: http://www.dms.umontreal.ca/andrew/PDF/BookChaps1n2.pdf, 2014.Google Scholar
Harper, A., Sharp conditional bounds for moments of the Riemann zeta function. Preprint, 2014.Google Scholar
Harper, A. J., Nikeghbali, A. and Radziwill, M., A note on Helson’s conjecture on moments of random multiplicative functions. Analytic Number Theory, Conf. in honor of Helmut Maier’s 60th birthday, to appear.Google Scholar
Heap, W. and Lindqvist, S., Moments of random multiplicative functions and truncated characteristic polynomials. Q. J. Math. (to appear).Google Scholar
Louboutin, S., Sur le calcul numérique des constantes des équations fonctionnelles des fonctions L associées aux caractères impairs. C. R. Acad. Sci. Paris Sér. I Math. 329 1999, 347–350.Google Scholar
Louboutin, S. and Munsch, M., The second and fourth moments of theta functions at their central point. J. Number Theory 133 2013, 1186–1193.CrossRefGoogle Scholar
Louboutin, S. and Munsch, M., On positive real zeros of theta and L-functions associated with real, even and primitive characters. Publ. Math. Debrecen 83 2013, 643–665.CrossRefGoogle Scholar
Munsch, M. and Shparlinski, I. E., Upper and lower bounds for higher moments of theta functions. Q. J. Math. 67 2016, 53–73.Google Scholar
Murty, R. M. and Murty, K. V., Non-vanishing of L-functions and Applications (Progress in Mathematics 157 ), Birkhäuser (Basel, 1997).Google Scholar
Rudnick, Z. and Soundararajan, K., Lower bounds for moments of L-functions. Proc. Natl. Acad. Sci. USA 102 2005, 6837–6838.CrossRefGoogle ScholarPubMed
Selberg, A., Contributions to the theory of the Riemann zeta-function. Arch. Math. Naturvid. 48 1946, 89–155.Google Scholar
Sono, K., Upper bounds for the moments of derivatives of Dirichlet L-functions. Cent. Eur. J. Math. 12 2014, 848–860.Google Scholar
Soundararajan, K., Moments of the Riemann zeta function. Ann. of Math. (2) 170 2009, 981–993.CrossRefGoogle Scholar