Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T17:22:09.043Z Has data issue: false hasContentIssue false
  • English
  • Français

SHAPES OF POLYHEDRA, MIXED VOLUMES AND HYPERBOLIC GEOMETRY

Part of: Low-dimensional topology Polytopes and polyhedra

Published online by Cambridge University Press:  23 September 2016

François Fillastre  and
Ivan Izmestiev
François Fillastre
Affiliation:
Departement of Mathematics, University of Cergy-Pontoise, UMR CNRS 8088, F-95000 Cergy-Pontoise, France email [email protected]
Ivan Izmestiev
Affiliation:
Institut für Mathematik, Freie Universität Berlin, Arnimallee 2, D-14195 Berlin, Germany Department of Mathematics, University of Fribourg, Chemin du Musée 23, CH-1700 Fribourg Pérolles, Switzerland email [email protected]
Get access

Abstract

We generalize to higher dimensions the Bavard–Ghys construction of the hyperbolic metric on the space of polygons with fixed directions of edges. The space of convex 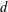$d$-dimensional polyhedra with fixed directions of facet normals has a decomposition into type cones that correspond to different combinatorial types of polyhedra. This decomposition is a subfan of the secondary fan of a vector configuration and can be analyzed with the help of Gale diagrams. We construct a family of quadratic forms on each of the type cones using the theory of mixed volumes. The Alexandrov–Fenchel inequalities ensure that these forms have exactly one positive eigenvalue. This introduces a piecewise hyperbolic structure on the space of similarity classes of polyhedra with fixed directions of facet normals. We show that some of the dihedral angles on the boundary of the resulting cone-manifold are equal to 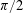$\unicode[STIX]{x1D70B}/2$.

MSC classification

Primary: 52B11: $n$-dimensional polytopes
Secondary: 52B35: Gale and other diagrams 57M50: Geometric structures on low-dimensional manifolds
Type
Research Article
Information
Mathematika , Volume 63 , Issue 1 , 2017 , pp. 124 - 183
Copyright
Copyright © University College London 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alexandrov, A. D., On the theory of mixed volumes II. Mat. Sb. 44 1937, 1205–1238 (Engl. transl. in [ 3 ]).Google Scholar
Alexandrov, A. D., Existence of a convex polyhedron and of a convex surface with a given metric. Mat. Sb., N. Ser. 11(53) 1942, 15–65 (Russian, English summary).Google Scholar
Alexandrov, A. D., Selected Works. Part I (Classics of Soviet Mathematics 4 ), Gordon and Breach Publishers (Amsterdam, 1996) ; selected scientific papers. Translated from the Russian by P. S. V. Naidu. Edited and with a preface by Yu. G. Reshetnyak and S. S. Kutateladze.Google Scholar
Bavard, C. and Ghys, É., Polygones du plan et polyèdres hyperboliques. Geom. Dedicata 43(2) 1992, 207–224.Google Scholar
Billera, L. J., Filliman, P. and Sturmfels, B., Constructions and complexity of secondary polytopes. Adv. Math. 83(2) 1990, 155–179.CrossRefGoogle Scholar
Billera, L. J., Gel’fand, I. M. and Sturmfels, B., Duality and minors of secondary polyhedra. J. Combin. Theory Ser. B 57(2) 1993, 258–268.Google Scholar
Bobenko, A. I. and Izmestiev, I., Alexandrov’s theorem, weighted Delaunay triangulations, and mixed volumes. Ann. Inst. Fourier (Grenoble) 58(2) 2008, 447–505.CrossRefGoogle Scholar
Bobenko, A. I. and Springborn, B. A., A discrete Laplace–Beltrami operator for simplicial surfaces. Discrete Comput. Geom. 38(4) 2007, 740–756.Google Scholar
De Loera, J. A., Rambau, J. and Santos, F., Triangulations: Structures for algorithms and applications. In Algorithms and Computation in Mathematics, Vol. 25, Springer (Berlin, 2010).Google Scholar
Ewald, G., Combinatorial Convexity and Algebraic Geometry (Graduate Texts in Mathematics 168 ), Springer (New York, 1996).Google Scholar
Fillastre, F., From spaces of polygons to spaces of polyhedra following Bavard, Ghys and Thurston. Enseign. Math. (2) 57(1–2) 2011, 23–56.Google Scholar
Fillastre, F., Fuchsian convex bodies: basics of Brunn–Minkowski theory. Geom. Funct. Anal. 23(1) 2013, 295–333.Google Scholar
Fillastre, F., Polygons of the Lorentzian plane and spherical simplexes. Elem. Math. 69 2014, 144–155.Google Scholar
Fillastre, F. and Izmestiev, I., Hyperbolic cusps with convex polyhedral boundary. Geom. Topol. 13(1) 2009, 457–492.Google Scholar
Fillastre, F. and Izmestiev, I., Gauss images of hyperbolic cusps with convex polyhedral boundary. Trans. Amer. Math. Soc. 363(10) 2011, 5481–5536.Google Scholar
Gelf́and, I. M., Kapranov, M. M. and Zelevinsky, A. V., Discriminants, resultants, and multidimensional determinants. In Mathematics: Theory and Applications, Birkhäuser Boston Inc. (Boston, MA, 1994).Google Scholar
Grünbaum, B., Convex Polytopes,, 2nd edn (Graduate Texts in Mathematics 221 ), Springer (New York, 2003) ; prepared and with a preface by V. Kaibel, V. Klee and G. M. Ziegler.Google Scholar
Im Hof, H.-C., Napier cycles and hyperbolic Coxeter groups. Bull. Soc. Math. Belg. Sér. A 42(3) 1990, 523–545 ; Algebra, groups and geometry.Google Scholar
Indermitte, C., Liebling, T. M., Troyanov, M. and Clémençon, H., Voronoi diagrams on piecewise flat surfaces and an application to biological growth. Theoret. Comput. Sci. 263(1–2) 2001, 263–274 ; Combinatorics and computer science (Palaiseau, 1997).Google Scholar
Izmestiev, I., The Colin de Verdière number and graphs of polytopes. Israel J. Math. 178 2010, 427–444.Google Scholar
Izmestiev, I., Infinitesimal rigidity of convex polyhedra through the second derivative of the Hilbert–Einstein functional. Canad. J. Math. 66(4) 2014, 783–825.Google Scholar
Kapovich, M. and Millson, J., On the moduli space of polygons in the Euclidean plane. J. Differential Geom. 42(2) 1995, 430–464.Google Scholar
Kapovich, M. and Millson., J. J., The symplectic geometry of polygons in Euclidean space. J. Differential Geom. 44(3) 1996, 479–513.Google Scholar
Khovanskii, A. G. and Timorin, V., On the theory of coconvex bodies. Discrete Comput. Geom. 52(4) 2014, 806–823.Google Scholar
Kubota, T., Über die Eibereiche im n-dimensionalen Raume. Sci. Rep. Tôhoku Univ. 14(1) 1925, 399–402.Google Scholar
Masur, H. and Smillie, J., Hausdorff dimension of sets of nonergodic measured foliations. Ann. of Math. (2) 134(3) 1991, 455–543.Google Scholar
McMullen, P., Representations of polytopes and polyhedral sets. Geom. Dedicata 2 1973, 83–99.Google Scholar
McMullen, P., Transforms, diagrams and representations. In Contributions to Geometry (Proc. Geom. Sympos., Siegen, 1978), Birkhäuser (Basel, 1979), 92–130.Google Scholar
McMullen, P., The polytope algebra. Adv. Math. 78(1) 1989, 76–130.Google Scholar
McMullen, P., Weights on polytopes. Discrete Comput. Geom. 15(4) 1996, 363–388.Google Scholar
McMullen, P. and Schneider, R., Valuations on convex bodies. In Convexity and its Applications, Birkhäuser (Basel, 1983), 170–247.Google Scholar
McMullen, P., Schneider, R. and Shephard, G. C., Monotypic polytopes and their intersection properties. Geom. Dedicata 3 1974, 99–129.Google Scholar
Minkowski, H., Volumen und Oberfläche. Math. Ann. 57 1903, 447–495.Google Scholar
Nishi, H. and Ohshika, K., A pseudo-metric on moduli space of hyperelliptic curves. Josai Math. Monogr. 5 2012, 51–59.Google Scholar
Postnikov, A., Reiner, V. and Williams, L., Faces of generalized permutohedra. Doc. Math. 13 2008, 207–273.Google Scholar
Pukhlikov, A. V. and Khovanskiĭ, A. G., Finitely additive measures of virtual polyhedra. Algebra i Analiz 4(2) 1992, 161–185.Google Scholar
Schneider, R., Das Christoffel-problem für polytope. Geom. Dedicata 6(1) 1977, 81–85.CrossRefGoogle Scholar
Schneider, R., Convex Bodies: the Brunn–Minkowski Theory (Encyclopedia of Mathematics and its Applications 44 ), Cambridge University Press (Cambridge, 1993).Google Scholar
Shephard, G. C., Decomposable convex polyhedra. Mathematika 10 1963, 89–95.Google Scholar
Stanley, R., The number of faces of a simplicial convex polytope. Adv. Math. 35 1980, 236–238.Google Scholar
Thurston, W. P., Three-Dimensional Geometry and Topology, Vol 1 (Princeton Mathematical Series  35 ) (ed. Levy, Silvio), Princeton University Press (Princeton, NJ, 1997).Google Scholar
Thurston, W. P., Shapes of polyhedra and triangulations of the sphere. In The Epstein Birthday Schrift (Geometry & Topology Monographs 1 ), Geometry Topology Publ. (Coventry, 1998), 511–549.Google Scholar
Troyanov, M., On the moduli space of singular Euclidean surfaces. In Handbook of Teichmüller Theory, Vol. I (IRMA Lectures Mathematics and Theoretical Physics 11 ), European Mathematical Society (Zürich, 2007), 507–540.Google Scholar
Veech, W. A., Flat surfaces. Amer. J. Math. 115(3) 1993, 589–689.Google Scholar
Wagner, U., k-sets and k-facets. In Surveys on Discrete and Computational Geometry (Contemporary Mathematics 453 ), American Mathematical Society (Providence, RI, 2008), 443–513.Google Scholar
Ziegler, G. M., Lectures on Polytopes (Graduate Texts in Mathematics 152 ), Springer (New York, 1995).Google Scholar