Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-28T05:06:49.918Z Has data issue: false hasContentIssue false
  • English
  • Français

Sections and projections of convex polytopes

Published online by Cambridge University Press:  26 February 2010

G. C. Shephard
G. C. Shephard
Affiliation:
University of East Anglia, Norwich NOR 88C, England.
Get access

Extract

Introduction. Gale diagrams, and similar techniques, have been used in several recent investigations into the combinatorial properties of convex polytopes. Here we describe other applications, namely to problems concerning sections and projections of polytopes of a given combinatorial type. 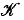For example, in §4 we shall show that every n–dimensional convex polytope with at most n + 2 vertices possesses the universal shadow boundary (usb) property: If is a subcomplex of the boundary complex ℬ (P) of P, and set 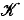is homeomorphic to an (n – 2)-sphere, then there exists a polytope P', combinatorially isomorphic to P, such that the complex 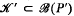corresponding to 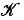is a shadow boundary of P'. We shall also show that this is the best possible result in that polytopes with n + 3 or more vertices do not, in general, have the usb property. A second application of the method, to be described in §5, is to the construction of non-realisable complexes.

Type
Research Article
Information
Mathematika , Volume 19 , Issue 2 , December 1972 , pp. 144 - 162
Copyright
Copyright © University College London 1972

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Barnette, D. W., “Projections of 3-polytopes”, Israel J. Math., 8 (1970), 304–308.Google Scholar
2.Bruggesser, H. and Mani, P., “Shellable decompositions of cells and spheres”, Math. Scand., 29 (1972), 197–205.Google Scholar
3.Grünbaum, B., Convex Polytopes (London-New York-Sydney, 1967).Google Scholar
4.Grünbaum, B., and Sreedharan, V. P., “An enumeration of simplicial 4-polytopes with 8 vertices”, J. Combinatorial Theory, 2 (1967), 437–465.Google Scholar
5.McMullen, P., “Representations of polytopes and polyhedral sets”, (to be published).Google Scholar
6.McMullen, P. and Shephard, G. C., Convex Polytopes and the Upper Bound Conjecture, London Mathematical Society Lecture Notes, Volume 3 (Cambridge, 1971)Google Scholar
7.McMullen, P., Schneider, R. and Shephard, G. C., “Monotypic polytopes and their intersection properties”, (to be published).Google Scholar
8.Shephard, G. C., “Diagrams for positive bases”, J. London Math. Soc., (2), 4 (1971), 165–175.CrossRefGoogle Scholar
9.Shephard, G. C., “Polyhedral diagrams for sections of the non-negative orthant”, Mathematika, 18 (1971), 255–263.Google Scholar