Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T22:30:11.056Z Has data issue: false hasContentIssue false
  • English
  • Français

Riemann equivalence of functions

Published online by Cambridge University Press:  26 February 2010

H. Kestelman
H. Kestelman
Affiliation:
University College, London
Get access

Extract

Two finite real functions ƒ(x) and g(x), defined for — ∞ < x < ∞, are said to be Riemann equivalent if |ƒ(x)—g(x)| has a zero Riemann integral over every finite interval; we then write ƒ~g or

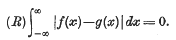
N. G. de Bruijn conjectured that if ƒ(x+h)~ƒ(x) for every real number h, then ƒ~c where c is a constant; this was proved by P. Erdös [1]. In this note we associate with an arbitrary function ƒ the additive group 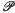(ƒ) of all numbers h which make ƒ(x)~ƒ(x+h), i.e. which make

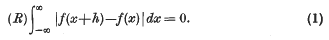
Type
Research Article
Information
Mathematika , Volume 2 , Issue 2 , December 1955 , pp. 97 - 104
Copyright
Copyright © University College London 1955

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Erdös, P., “A theorem on the Riemann integral”, Indag. Math., 14, No. 2 (1952), 142–144.CrossRefGoogle Scholar
2.Souslin, M., “Sur un corps non-dénombrable de nombres réels”, Fundamenta Math., 4 (1923), 311–315.CrossRefGoogle Scholar
3.Sierpiński, W., “… la Base de M. Hamel”, Fundamenta Math., 1 (1920), 105–111.CrossRefGoogle Scholar
4.Sierpiński, W. “Hypothèse du Continu”, Warsaw, 1934.Google Scholar
5.Steinhaus, H., “Sur les distances…”, Fundamenta Math., 1 (1920), 93–104.CrossRefGoogle Scholar