Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T16:30:53.907Z Has data issue: false hasContentIssue false
  • English
  • Français

RANDOMNESS AND NON-RANDOMNESS PROPERTIES OF PIATETSKI-SHAPIRO SEQUENCES MODULO 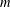$m$

Part of: Multiplicative number theory Sequences and sets Exponential sums and character sums Probabilistic theory: distribution modulo $1$; metric theory of algorithms

Published online by Cambridge University Press:  14 August 2019

Jean-Marc Deshouillers ,
Michael Drmota ,
Clemens Müllner  and
Lukas Spiegelhofer
Jean-Marc Deshouillers
Affiliation:
Université de Bordeaux, CNRS, Bordeaux INP, IMB, UMR 5251, F-33400, Talence, France email [email protected]
Michael Drmota
Affiliation:
Institut für Diskrete Mathematik und Geometrie, TU Wien, Wiedner Hauptstr. 8–10, 1040 Wien, Austria email [email protected]
Clemens Müllner
Affiliation:
Institut für Diskrete Mathematik und Geometrie, TU Wien, Wiedner Hauptstr. 8–10, 1040 Wien, Austria CNRS, Université de Lyon, Université Lyon 1, Institut Camille Jordan, 43 boulevard du 11 novembre 1918, 69622 Villeurbanne Cedex, France email [email protected]
Lukas Spiegelhofer
Affiliation:
Institut für Diskrete Mathematik und Geometrie, TU Wien, Wiedner Hauptstr. 8–10, 1040 Wien, Austria email [email protected]
Get access

Abstract

We study Piatetski-Shapiro sequences 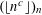$(\lfloor n^{c}\rfloor )_{n}$ modulo 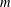$m$, for non-integer 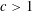$c>1$ and positive 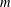$m$, and we are particularly interested in subword occurrences in those sequences. We prove that each block 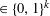$\in \{0,1\}^{k}$ of length 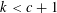$k<c+1$ occurs as a subword with the frequency 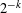$2^{-k}$, while there are always blocks that do not occur. In particular, those sequences are not normal. For 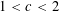$1<c<2$, we estimate the number of subwords from above and below, yielding the fact that our sequences are deterministic and not morphic. Finally, using the Daboussi–Kátai criterion, we prove that the sequence 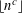$\lfloor n^{c}\rfloor$ modulo 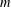$m$ is asymptotically orthogonal to multiplicative functions bounded by 1 and with mean value 0.

MSC classification

Primary: 11B50: Sequences (mod $m$) 11B83: Special sequences and polynomials
Secondary: 11K16: Normal numbers, radix expansions, Pisot numbers, Salem numbers, good lattice points, etc. 11L07: Estimates on exponential sums 11N37: Asymptotic results on arithmetic functions
Type
Research Article
Information
Mathematika , Volume 65 , Issue 4 , 2019 , pp. 1051 - 1073
Copyright
Copyright © University College London 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was supported by the Austrian Science Foundation FWF, SFB F5502-N26 “Subsequences of Automatic Sequences and Uniform Distribution”, which is a part of the Special Research Program “Quasi Monte Carlo Methods: Theory and Applications”, by the joint ANR-FWF project ANR-14-CE34-0009, I-1751 MuDeRa, Ciência sem Fronteiras (project PVE 407308/2013-0) and by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme under the Grant Agreement No. 648132.

References

Alessandri, P. and Berthé, V., Three distance theorems and combinatorics on words. Enseign. Math. (2) 44(1–2) 1998, 103–132.Google Scholar
Allouche, J.-P. and Shallit, J., Automatic Sequences: Theory, Applications, Generalizations, Cambridge University Press (Cambridge, 2003).10.1017/CBO9780511546563Google Scholar
Baker, R. C., Banks, W. D., Brüdern, J., Shparlinski, I. E. and Weingartner, A. J., Piatetski-Shapiro sequences. Acta Arith. 157(1) 2013, 37–68.10.4064/aa157-1-3Google Scholar
Deshouillers, J.-M., Sur la répartition des nombres [n c ] dans les progressions arithmétiques. C. R. Acad. Sci. Paris Sér. A–B 277 1973, A647–A650.Google Scholar
Deshouillers, J.-M., Drmota, M. and Morgenbesser, J. F., Subsequences of automatic sequences indexed by ⌊n c ⌋ and correlations. J. Number Theory 132(9) 2012, 1837–1866.10.1016/j.jnt.2012.03.006Google Scholar
Drmota, M. and Tichy, R. F., Sequences, Discrepancies and Applications (Lecture Notes in Mathematics 1651 ), Springer (Berlin, 1997).10.1007/BFb0093404Google Scholar
Erdős, P. and Turán, P., On a problem in the theory of uniform distribution. I. Nederl. Akad. Wetensch. Proc. 51 1948, 1146–1154 = Indag. Math. 10 (1948), 370–378.Google Scholar
Graham, S. W. and Kolesnik, G., Van der Corput’s Method of Exponential Sums (London Mathematical Society Lecture Note Series 126 ), Cambridge University Press (Cambridge, 1991).10.1017/CBO9780511661976Google Scholar
Kátai, I., A remark on a theorem of H. Daboussi. Acta Math. Hungar. 47(1–2) 1986, 223–225.10.1007/BF01949145Google Scholar
Koksma, J. F., Some theorems on Diophantine inequalities. Scriptum 5, Mathematisch Centrum Amsterdam, 1950.Google Scholar
Lang, S., Introduction to Transcendental Numbers, Addison-Wesley (Reading, MA–London–Don Mills, ON, 1966).Google Scholar
Leitmann, D. and Wolke, D., Primzahlen der Gestalt [f (n)]. Math. Z. 145(1) 1975, 81–92.10.1007/BF01214500Google Scholar
Mauduit, C. and Rivat, J., Propriétés q-multiplicatives de la suite ⌊n c ⌋, c > 1. Acta Arith. 118(2) 2005, 187–203.10.4064/aa118-2-6+1.+Acta+Arith.+118(2)+2005,+187–203.10.4064/aa118-2-6>Google Scholar
Mauduit, C., Rivat, J. and Sárközy, A., On the pseudo-random properties of n c . Illinois J. Math. 46(1) 2002, 185–197.10.1215/ijm/1258136149Google Scholar
Mignosi, F., On the number of factors of Sturmian words. Theoret. Comput. Sci. 82(1, Algorithms Automat. Complexity Games) 1991, 71–84.10.1016/0304-3975(91)90172-XGoogle Scholar
Müllner, C. and Spiegelhofer, L., Normality of the Thue–Morse sequence along Piatetski-Shapiro sequences, II. Israel J. Math. 220(2) 2017, 691–738.10.1007/s11856-017-1531-xGoogle Scholar
Piatetski-Shapiro, I. I., On the distribution of prime numbers in sequences of the form [f (n)]. Mat. Sb. (N.S.) 33(75) 1953, 559–566.Google Scholar
Ramachandra, K., Contributions to the theory of transcendental numbers. I, II. Acta Arith. 14 1967–1968, 65–72; Acta Arith. 14 (1967–1968), 73–88.10.4064/aa-14-1-65-72Google Scholar
Rieger, G. J., Uber die natürlichen und primen Zahlen der Gestalt [n c ] in arithmetischer Progression. Arch. Math. (Basel) 18 1967, 35–44.10.1007/BF01899471Google Scholar
Rivat, J. and Sargos, P., Nombres premiers de la forme ⌊n c ⌋. Canad. J. Math. 53(2) 2001, 414–433.10.4153/CJM-2001-017-0Google Scholar
Sarnak, P., Mobius randomness and dynamics. Not. S. Afr. Math. Soc. 43(2) 2012, 89–97.Google Scholar
Spiegelhofer, L., The level of distribution of the Thue–Morse sequence. Preprint, 2018, arXiv:1803.01689.Google Scholar
Szüsz, P., On a problem in the theory of uniform distribution. In C. R. Premier Congrès Math. Hongrois, Akadémiai Kiadó (Budapest, 1952), 461–473; in Hungarian.Google Scholar