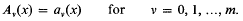A property of polynomials over a finite field

Extract

Let q be a power of an odd prime, [q] denote the Galois field GF(q) and write X(x) = x^q − x. Let f(x) be a polynomial, having no linear factors, over [q], of positive degree, and write 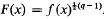. Consider the continued fraction expansions

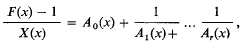
and

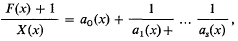
where the A_i(x) and a_j,(x) are polynomials over [q] of degree ≥ 1 (if i ≥ 1, j ≥ 1). Plainly A₀(x) = a_o(x). Suppose that n = n_f is the integer denned uniquely as the largest m such that