Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T05:46:04.676Z Has data issue: false hasContentIssue false
  • English
  • Français

Prolongations of valuations to simple transcendental extensions with given residue field and value group

Part of: Field extensions

Published online by Cambridge University Press:  26 February 2010

Sudesh K. Khanduja
Sudesh K. Khanduja
Affiliation:
Dr. S. K. Khanduja, Centre for Advanced Study in Mathematics, Panjab University, Chandigarh–160014, India.
Get access

Abstract

Let K0(x) be a simple transcendental extension of a field K0, υ0 be a valuation of K0 with value group G0 and residue field K0. Suppose 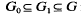is an inclusion of totally ordered abelian groups with [G1: G0] < ∞ such that G is the direct sum of G1 and an infinite cyclic group. It is proved that there exists an (explicitly constructible) valuation υ of K0(x) extending υ0 such that the value group of υ is G and its residue field is k, where k is a given finite extension of k0. This is analogous to a result of Matignon and Ohm [2, Corollary 3.2] for residually non-algebraic prolongations of υ0 to K0(x).

MSC classification

Secondary: 12F20: Transcendental extensions
Type
Research Article
Information
Mathematika , Volume 38 , Issue 2 , December 1991 , pp. 386 - 390
Copyright
Copyright © University College London 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Khanduja, S. K.. Value groups and simple transcendental extensions, Mathematika, 38 (1991), 381–385.CrossRefGoogle Scholar
2.Matignon, M. and Ohm, J.. A structure theorem for extensions of valued fields. Proc. Amer. Math. Soc, 104 (1988), 392–402.CrossRefGoogle Scholar
3.Nagata, M.. A theorem on valuation rings and its applications. Nagoya Math. J., 29 (1967), 85–91.CrossRefGoogle Scholar
4.Ohm, J.. The ruled residue theorem for simple transcendental extensions of valued fields. Proc. Amer. Math. Soc, 89 (1983), 16–18.CrossRefGoogle Scholar
5.Ohm, J.. Simple transcendental extensions of valued fields II: A fundamental inequality. J Math. Kyoto Univ., 25 (1985), 583–596.Google Scholar
6.Zariski, O. and Samuel, P.. Commutative Algebra II (Van Nostrand, Princeton, 1960).CrossRefGoogle Scholar