Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T06:08:49.724Z Has data issue: false hasContentIssue false
  • English
  • Français

A presentation of SL2 for Euclidean imaginary quadratic number fields

Published online by Cambridge University Press:  26 February 2010

P. M. Cohn
P. M. Cohn
Affiliation:
Bedford College, University of London and Rutgers, The State University.
Get access

Extract

Let G be any group and G′ its derived, then G/G′—the group G made abelian—will be denoted by Ga. Over any ring R, denote by E2(R) the group generated by the matrices 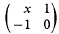as x ranges over R; the structure of E2(R)a has been described in a recent theorem [2; Th. 9.3] for certain rings R, the “quasi-free rings for GE2” (cf. §2 below). Now over a commutative Euclidean domain, E2(R) is just the special linear group SL2(R); this suggests applying the theorem to the ring of integers in a Euclidean number field. However, the only number fields whose rings were shown to be quasi-free for GE2 in [2] were the non-Euclidean imaginary quadratic fields. In fact that leaves the application of Th. 9.3 of [2] to the ring of Gaussian integers unjustified (I am indebted to J.-P. Serre for drawing this oversight to my attention). In order to justify this application one would have to show either (a) that the Gaussian integers are quasi-free for GE2., or (b) that Th. 9.3 of [2] holds under weaker hypotheses which are satisfied by the Gaussian integers. Our object in this note is to establish (b)–indeed our only course, since the Gaussian integers turn out to be not quasi-free.

Type
Research Article
Information
Mathematika , Volume 15 , Issue 2 , December 1968 , pp. 156 - 163
Copyright
Copyright © University College London 1968

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Bianchi, L., “Sui gruppi di sostituzioni lineari con coefficient appartenenti a corpi quadratici immaginari”, Math. Ann., 40 (1892), 332–412.CrossRefGoogle Scholar
2.Cohn, P. M., “On the structure of the GL2 of a ring”, Publ. Math. IHES., No. 30 (Paris, 1966).CrossRefGoogle Scholar
3.Hurwitz, A., “Über die Entwicklung komplexer Grössen in Kettenbrüche”, Acta Math., 11 (1887–1888), 187–200, or Math. Werke II(Basel, 1933), 72.CrossRefGoogle Scholar
4.Magnus, W., Karrass, A. and Solitar, D., Combinatorial group theory (Interscience, New York, 1966).Google Scholar
5.Serre, J.-P., “Le problème des groupes de congruence pour SL2”, to appear.Google Scholar
6.Silvester, J. R., unpublished.Google Scholar
7.Swan, R. G., “Generators and relations for certain special linear groups”, to appear.Google Scholar