Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-28T08:54:53.315Z Has data issue: false hasContentIssue false
  • English
  • Français

Positive solutions for Dirichlet problems of singular quasilinear elliptic equations via variational methods

Part of: Elliptic equations and systems

Published online by Cambridge University Press:  26 February 2010

Ravi P. Agarwal ,
Haishen Lü  and
Donal O'Regan
Ravi P. Agarwal
Affiliation:
Department of Mathematical Sciences, Florida Institute of Technology, Melbourne, FL 32901-6975, U.S.A.
Haishen Lü
Affiliation:
Department of Applied Mathematics, Hohai University, Nanjing, 210098, China.
Donal O'Regan
Affiliation:
Department of Mathematics, National University of Ireland, Galway, Ireland.
Get access

Abstract

This paper studies the existence and multiplicity of positive solutions of the following problem:

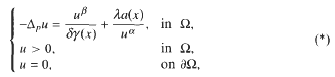
where Ω⊂RN(N≥3) is a smooth bounded domain, 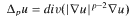, 1 < p < N, and 0 < α < 1, p - 1 < β < p* - 1 (p* = Np/(N - p)) and 0 < γ < N + ((β + 1)(p - N)/p) are three constants. Also δ(x) = dist(x, ∂Ω), a ∈ Lp and λ < 0 is a real parameter. By using the direct method of the calculus of variations, Ekeland's Variational Principle and an idea of G. Tarantello, it is proved that problem (*) has at least two positive weak solutions if λ is small enough.

MSC classification

Secondary: 35J20: Variational methods for second-order elliptic equations
Type
Research Article
Information
Mathematika , Volume 51 , Issue 1-2 , December 2004 , pp. 187 - 202
Copyright
Copyright © University College London 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Ambrosetti, A., Brezis, H. and Cerami, G.. Combined effects of concave and convex nonlinearities in some elliptic problems. J. Fund. Anal, 122 (1994), 519–543.Google Scholar
2.Ambrosetti, A., Azorero, J. G. and Peral, I.. Multiplicity results for some nonlinear elliptic equations. J. Fund. Anal., 137 (1996), 219–242.Google Scholar
3.Tarantello, G.. On nonhomogeneous elliptic equations involving critical Soblev exponent. Ann. hist. H. Poincare Anal. Nonlineaire, 9 (1992), 281–304.Google Scholar
4.Sun, Y., Wu, S. and Long, Y.. Combined effects of singular and superlinear nonlinearities in some singular boundary value problems. J. Diff. Eqns., 176 (2001), 511–531.Google Scholar
5.Crandall, M. G., Rabinowitz, P. H. and Tartar, L.. On a Dirichlet problem with a singular nonlinearity, Comm. Partial Diff. Eqns., 2 (1977), 193–222.Google Scholar
6.Struwe, M.. Varialionul Methods. Springer-Verlag (New York-Berlin, 1990).Google Scholar
7.Lair, A. V. and Shaker, A. W.. Classical and weak solutions of a singular semilinear elliptic problem. J. Math. Anal. Appl., 211 (1997), 193–222.Google Scholar
8.Lazer, A. C. and McKenna, P. J.. On a singular nonlinear elliptic boundary value problem. Proc. Amer. Math. Soc., 111 (1991), 721–730.Google Scholar
9.Agarwal, P. P. and O'Regan, D.. Singular Differential and Integral Equations with Applications. Kluwer Academic Publishers (Dordrecht, 2003).Google Scholar
10.Shi, J. and Yao, M.. On a singular nonlinear semilinear elliptic problem. Proc. Roy. Soc. Edinburgh A, 128 (1998), 1389–1401.Google Scholar
11.Coclite, M. M. and Palmieri, G.. On a singular nonlinear Dirichlet problems. Comm. Partial Diff. Eqns., 14 (1989), 1315–1327.Google Scholar
12.Shaker, A. W.. On singular semilinear elliptic equations. J. Math. Anal. Appl., 173 (1993). 222–228.Google Scholar
13.Diaz, J. I., Morel, J. M. and Oswald, L.. An elliptic equation with singular nonlineurity. Comm Partial Diff. Eqns., 12 (1987), 1333–1344.Google Scholar
14.Drábek, P., Kreji, P. and Takac, P.. Nonlinear Differential Equations. CRC Press (Boca Raton. FL, 2000).Google Scholar
15.Triebel, H.. Interpolation Theory, Function Spaces, Differential Operators. North Holland (Amsterdam, 1978).Google Scholar
16.Galakhov, E.. On some quasilinear PDE's with singularities on the boundary. Diff. Integ. Eqns., 15 (2002), 1153–1169.Google Scholar
17.Cui, S.. Existence and nonexistence of positive solutions for singular semilinear elliptic boundary value problems. Nonlinear Anal., 41 (2000), 149–176.Google Scholar
18.Fučik, S. and Kufner, A.. Nonlinear Differential Equations. Elsevier (Holland, 1980).Google Scholar