Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Granville, Andrew
Shparlinski, Igor E.
and
Zaharescu, Alexandru
2005.
On the distribution of rational functions along a curve over Fp and residue races.
Journal of Number Theory,
Vol. 112,
Issue. 2,
p.
216.
Shparlinski, Igor E.
2012.
Modular hyperbolas.
Japanese Journal of Mathematics,
Vol. 7,
Issue. 2,
p.
235.
Chaubey, Sneha
Tamazyan, Albert
and
Zaharescu, Alexandru
2019.
Lattice point problems involving index and joint visibility.
Proceedings of the American Mathematical Society,
Vol. 147,
Issue. 8,
p.
3273.


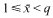 be such that
be such that 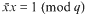 . For fixed
. For fixed