Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-27T06:13:20.534Z Has data issue: false hasContentIssue false
  • English
  • Français

OPPOSITE-SIGN KLOOSTERMAN SUM ZETA FUNCTION

Part of: Exponential sums and character sums Zeta and $L$-functions: analytic theory Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  28 January 2016

Eren Mehmet Kıral
Eren Mehmet Kıral*
Affiliation:
Department of Mathematics, Texas A&M University, Mailstop 3368, College Station, TX 77843, U.S.A. email [email protected]
Get access

Abstract

We study the meromorphic continuation and the spectral expansion of the opposite-sign Kloosterman sum zeta function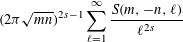

$$\begin{eqnarray}\displaystyle (2{\it\pi}\sqrt{mn})^{2s-1}\mathop{\sum }_{\ell =1}^{\infty }\frac{S(m,-n,\ell )}{\ell ^{2s}} & & \displaystyle \nonumber\end{eqnarray}$$
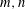for $m,n$ positive integers, to all 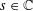$s\in \mathbb{C}$. There are poles of the function corresponding to zeros of the Riemann zeta function and the spectral parameters of Maass forms. The analytic properties of this function are rather delicate. It turns out that the spectral expansion of the zeta function converges only in a left half-plane, disjoint from the region of absolute convergence of the Dirichlet series, even though they both are analytic expressions of the same meromorphic function on the entire complex plane.

MSC classification

Primary: 11F66: Langlands $L$-functions; one variable Dirichlet series and functional equations 11F72: Spectral theory; Selberg trace formula 11L05: Gauss and Kloosterman sums; generalizations 11M36: Selberg zeta functions and regularized determinants; applications to spectral theory, Dirichlet series, Eisenstein series, etc. Explicit formulas
Type
Research Article
Information
Mathematika , Volume 62 , Issue 2 , 2016 , pp. 406 - 429
Copyright
Copyright © University College London 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Davenport, H., Multiplicative Number Theory, 3rd edn., (Graduate Texts in Mathematics 74 ), Springer (New York, 2000).Google Scholar
Goldfeld, D. and Sarnak, P., Sums of Kloosterman sums. Invent. Math. 71(2) 1983, 243–250.Google Scholar
Gradshteyn, I. S. and Ryzhik, I. M., Table of Integrals, Series, and Products, 8th edn., Elsevier/Academic Press (Amsterdam, 2015).Google Scholar
Hoffstein, J., Hulse, T. A. and Reznikov, A., Multiple Dirichlet series and shifted convolutions. J. Number Theory 161 2016, 457–533.CrossRefGoogle Scholar
Motohashi, Y., On the Kloosterman-sum zeta-function. Proc. Japan Acad. Ser. A Math. Sci. 71(4) 1995, 69–71.Google Scholar
Motohashi, Y., Spectral Theory of the Riemann Zeta-function (Cambridge Tracts in Mathematics 127 ), Cambridge University Press (Cambridge, 1997), doi:10.1017/CBO9780511983399.Google Scholar
Sarnak, P. and Tsimerman, J., On Linnik and Selberg’s conjecture about sums of Kloosterman sums. In Algebra, Arithmetic, and Geometry: in Honor of Yu. I. Manin, Vol. II (Progress in Mathematics 270 ), Birkhäuser (Boston, MA, 2009), 619–635.CrossRefGoogle Scholar
Selberg, A., On the estimation of Fourier coefficients of modular forms. In Theory of Numbers (Proceedings of Symposia in Pure Mathematics VIII ), American Mathematical Society (Providence, RI, 1965), 1–15.Google Scholar
Titchmarsh, E. C., The Theory of the Riemann Zeta-function, Vol. 196, Oxford University Press (1951).Google Scholar