Article contents
On the positivity of solutions to the Smoluchowski equations
Published online by Cambridge University Press: 26 February 2010
Extract
The dynamics of cluster growth can be modelled by the following infinite system of ordinary differential equations, first proposed by Smoluchowski, [8],
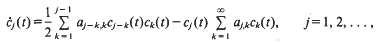
where cj=cj(t) represents the physical concentration of j-clusters (aggregates of j identical particles), aj,k=aj,k≥0 are the time-independent coagulation coefficients, measuring the effectiveness of the coagulation process between a j-cluster and a k-cluster, and the first sum in the right-hand side of (1) is defined to be zero if j = 1.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1995
References
- 3
- Cited by


