Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T07:00:06.404Z Has data issue: false hasContentIssue false
  • English
  • Français

On the group of automorphisms of the Euclidean hypersphere

Published online by Cambridge University Press:  26 February 2010

Adib A. Fadlalla
Adib A. Fadlalla
Affiliation:
Faculty of Science, Cairo University.
Get access

Extract

Let Cn be the n-dimensional complex number space of the complex variables z1,…, zn and 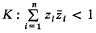be the unit hypersphere. Further, let G be the group of all holomorphic automorphisms of K, then G is a n(n + 2)-dimensional real Lie group. In [3] the author has proved that for any P∈∂K (the boundary of K) there exists a decomposition of G in the form 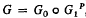, where G0 is the group of all analytic rotations about the origin and 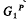is a 2n-dimensional real Lie group, whose underlying topological space is K, which acts transitively on K and P is a fixed point of all elements of .

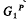Type
Research Article
Information
Mathematika , Volume 15 , Issue 2 , December 1968 , pp. 193 - 198
Copyright
Copyright © University College London 1968

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Behnke, und Thullen, , Theorie der Funktionen mehrerer Komplexer Veränderlichen, Erg. Math., 3 (Berlin, 1934).Google Scholar
2.Fadlalla, A. A., “The Carathéodory limiting spherical shells in the Euclidean hypersphere”, Mathematika, 13 (1966), 69–75.CrossRefGoogle Scholar
3.Fadlalla, A. A. “On the group of automorphisms of the Euclidean hypersphere”, Quart. J. Math., Oxford (2), 18 (1967), 97–101.CrossRefGoogle Scholar
4.Osgood, , Lehrbuch der Funktionentheorie II, 2 aufl (1929).Google Scholar
5.Sperner, E., Einfiihrung in die analytische Geometrie und Algebra, 2 Teil, 3 aufl (Göottingen, 1959).Google Scholar