Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T05:05:18.087Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Galois groups of the iterates of x2+1

Published online by Cambridge University Press:  26 February 2010

J. E. Cremona
J. E. Cremona
Affiliation:
Department of Mathematics, University of Exeter, North Park Road, Exeter. EX4 4QE.
Get access

Extract

§1. Introduction. In [1], Odoni discusses the iterates of the polynomial x2 +1 and their Galois groups over the rationals 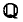(a problem initially proposed by J. McKay). Setting f1,(x) = x2+1 and fn(x) =f1(fn-1(X)) for n ≥ 2, write Kn for the splitting field of fn(x) over 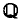and Ωn = Gal (Kn/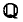). Then Odoni proves that Ωn is isomorphic to a subgroup of [C2]n, the nth wreath power of the cyclic group C2 of order 2, and gives a simple rational criterion for Ωn 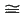[C2]n to hold. In this note we describe a computer implementation of Odoni's criterion, and state the result that Ωn 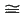[C2]n for n ≤ 5 × 107.

Type
Research Article
Information
Mathematika , Volume 36 , Issue 2 , December 1989 , pp. 259 - 261
Copyright
Copyright © University College London 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Odoni, R. W. K.. Realising wreath products of cyclic groups as Galois groups. Mathematika, 35 (1988), 101–113.CrossRefGoogle Scholar