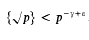Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Tolev, D.I.
1991.
On the simultaneous distribution of the fractional parts of different powers of prime numbers.
Journal of Number Theory,
Vol. 37,
Issue. 3,
p.
298.
Balog, Antal
and
Harman, Glyn
1991.
On mean values of Dirichlet polynomials.
Archiv der Mathematik,
Vol. 57,
Issue. 6,
p.
581.
Warnock, Tony T.
1995.
Monte Carlo and Quasi-Monte Carlo Methods in Scientific Computing.
Vol. 106,
Issue. ,
p.
354.
Zhai, Wenguang
2001.
On the Simultaneous Distribution of the Fractional Parts of Different Powers of Prime Numbers.
Journal of Number Theory,
Vol. 86,
Issue. 1,
p.
133.
Harman, Glyn
and
Lewis, Philip
2001.
Gaussian primes in narrow sectors.
Mathematika,
Vol. 48,
Issue. 1-2,
p.
119.
Narkiewicz, Władysław
2012.
Rational Number Theory in the 20th Century.
p.
13.
Cai, Yingchun
2013.
On the distribution of \documentclass{aastex} \usepackage{amsbsy} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{bm} \usepackage{mathrsfs} \usepackage{pifont} \usepackage{stmaryrd} \usepackage{textcomp} \usepackage{upgreek} \usepackage{portland,xspace} \usepackage{amsmath,amsxtra} \usepackage{bbm} \pagestyle{empty} \DeclareMathSizes{10}{9}{7}{6} \begin{document} \(\sqrt p\) \end{document} modulo one involving primes of special type.
Studia Scientiarum Mathematicarum Hungarica,
Vol. 50,
Issue. 4,
p.
470.
Dunn, Alexander
2017.
On the distribution of αp+β modulo one.
Journal of Number Theory,
Vol. 176,
Issue. ,
p.
67.
Shubin, A. V.
2020.
Fractional Parts of Noninteger Powers of Primes.
Mathematical Notes,
Vol. 108,
Issue. 3-4,
p.
394.
Malik, Amita
and
Prabhu, Neha
2022.
Equidistribution of αpθ$\alpha p^{\theta }$ with a Chebotarev condition and applications to extremal primes.
Mathematika,
Vol. 68,
Issue. 3,
p.
595.
Shubin, Andrei
2022.
Fractional Parts of Non-Integer Powers of Primes. II.
The Quarterly Journal of Mathematics,
Vol. 73,
Issue. 1,
p.
277.