On the classgroup of integral grouprings of finite Abelian groups II

Extract

In this note I settle a question which arose out of my first paper under the above title (cf. [1]), where I considered the classgroup C(Z(Γ)) of the integral groupring Z(Γ) of a finite Abelian group Γ. This classgroup maps onto the classgroup C(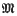) of the maximal order 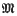of the rational groupring Q(Γ), and C(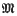) is the product of the ideal classgroups of the algebraic number fields which occur as components of Q(Γ) and is thus in a sense known. One is then interested in the kernel D(Z(Γ)) of C(Z(Γ)) → C(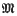) and in its order k(Γ). In [1] I proved that, for Γ a p-group, k(Γ) is a power of p. I also computed k(Γ) for small exponents. My computation used crucially the fact that, for the groups Γ considered, the groups of units of algebraic integers which occurred were finite, i.e. that the only number fields which turned up were Q and Q(n) with n⁴ = 1 or n⁶ = 1. The numerical results obtained led me to the question whether in fact k(Γ) tends to infinity with the order of Γ.