Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T14:56:17.554Z Has data issue: false hasContentIssue false
  • English
  • Français

ON ITERATED PRODUCT SETS WITH SHIFTS

Part of: Additive number theory; partitions Harmonic analysis in one variable

Published online by Cambridge University Press:  21 May 2019

Brandon Hanson ,
Oliver Roche-Newton  and
Dmitrii Zhelezov
Brandon Hanson
Affiliation:
University of Georgia, Athens, GA, U.S.A. email [email protected]
Oliver Roche-Newton
Affiliation:
Johann Radon Institute for Computational and Applied Mathematics, Linz, Austria email [email protected]
Dmitrii Zhelezov
Affiliation:
Alfréd Rényi Institute of Mathematics, Hungarian Academy of Sciences, Budapest, Hungary email [email protected]
Get access

Abstract

We prove that, for any finite set 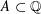$A\subset \mathbb{Q}$ with 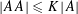$|AA|\leqslant K|A|$ and any positive integer 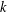$k$, the 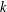$k$-fold product set of the shift 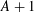$A+1$ satisfies the bound

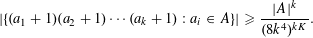$$\begin{eqnarray}|\{(a_{1}+1)(a_{2}+1)\cdots (a_{k}+1):a_{i}\in A\}|\geqslant \frac{|A|^{k}}{(8k^{4})^{kK}}.\end{eqnarray}$$
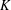This result is essentially optimal when $K$ is of the order 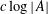$c\log |A|$, for a sufficiently small constant 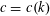$c=c(k)$. Our main tool is a multiplicative variant of the 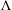$\unicode[STIX]{x1D6EC}$-constants used in harmonic analysis, applied to Dirichlet polynomials.

MSC classification

Primary: 11P70: Inverse problems of additive number theory, including sumsets 42A70: Trigonometric moment problems
Type
Research Article
Information
Mathematika , Volume 65 , Issue 4 , 2019 , pp. 831 - 850
Copyright
Copyright © University College London 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amoroso, F. and Viada, E., Small points on subvarieties of a torus. Duke Math. J. 150(3) 2009, 407–442.10.1215/00127094-2009-056Google Scholar
Beukers, F. and Schlickewei, H. P., The equation x + y = 1 in finitely generated groups. Acta Arith. 78(2) 1996, 189–199.10.4064/aa-78-2-189-199Google Scholar
Bourgain, J., More on sum-product phenomenon in prime fields and its applications. Int. J. Number Theory 1 2005, 1–32.10.1142/S1793042105000108Google Scholar
Bourgain, J. and Chang, M.-C., On the size of k-fold sum and product sets of integers. J. Amer. Math. Soc. 17(2) 2004, 473–497.10.1090/S0894-0347-03-00446-6Google Scholar
Chang, M.-C., The Erdős–Szemerédi problem on sum set and product set. Ann. of Math. (2) 157(3) 2003, 939–957.10.4007/annals.2003.157.939Google Scholar
Chang, M.-C., Sum and product of different sets. Contrib. Discrete Math. 1(1) 2006, 47–56.Google Scholar
Erdős, P. and Szemerédi, E., On sums and products of integers. In Studies in Pure Mathematics, Birkhäuser (Basel, 1983), 213–218.10.1007/978-3-0348-5438-2_19Google Scholar
Evertse, J. H., Győry, K., Stewart, C. L. and Tijdeman, R., On s-unit equations in two unknowns. Invent. Math. 92(3) 1988, 461–477.10.1007/BF01393743Google Scholar
Evertse, J.-H., Schlickewei, H. P. and Schmidt, W. M., Linear equations in variables which lie in a multiplicative group. Ann. of Math. (2) 155(3) 2002, 807–836.10.2307/3062133Google Scholar
Garaev, M. Z. and Shen, C.-Y., On the size of the set A (A + 1). Math. Z. 265(1) 2010, 125–132.10.1007/s00209-009-0504-0Google Scholar
Hanson, B., Roche-Newton, O. and Zhelezov, D., On iterated product sets with shifts II. Preprint, 2018, arXiv:1806.01697.10.1112/S0025579319000081Google Scholar
Jones, T. G. F. and Roche-Newton, O., Improved bounds on the set A (A + 1). J. Combin. Theory Ser. A 120(3) 2013, 515–526.10.1016/j.jcta.2012.11.001Google Scholar
Konyagin, S. V. and Shkredov, I. D., On sum sets of sets, having small product set. Proc. Steklov Inst. Math. 290 2015, 288–299.10.1134/S0081543815060255Google Scholar
Shakan, G., On higher energy decompositions and the sum-product phenomenon. Math. Proc. Cambridge Philos. Soc. (to appear). Preprint, 2018, arXiv:1803.04637.10.1017/S0305004118000506Google Scholar
Shkredov, I. D., Some remarks on sets with small quotient set. Sb. Math. 208(12) 2017, 144–158.10.1070/SM8733Google Scholar
Tao, T. and Vu, V., Additive Combinatorics, Cambridge University Press (2006).10.1017/CBO9780511755149Google Scholar
Zhelezov, D., Bourgain-Chang’s proof of the weak Erdős–Szemerédi conjecture. Preprint, 2017,arXiv:1710.09316.Google Scholar