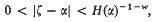Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Moran, W.
Pearce, C. E. M.
and
Pollington, A. D.
1992.
T‐numbers form anM0set.
Mathematika,
Vol. 39,
Issue. 1,
p.
18.
Bugeaud, Yann
2002.
Nombres de Liouville et nombres normaux.
Comptes Rendus. Mathématique,
Vol. 335,
Issue. 2,
p.
117.
Olsen, L.
and
Renfro, Dave L.
2006.
On the exact Hausdorff dimension of the set of Liouville numbers. II.
manuscripta mathematica,
Vol. 119,
Issue. 2,
p.
217.
Bugeaud, Yann
2008.
Diophantine Approximation.
Vol. 16,
Issue. ,
p.
107.
Bugeaud, Yann
2012.
Continued fractions with low complexity: transcendence measures and quadratic approximation.
Compositio Mathematica,
Vol. 148,
Issue. 3,
p.
718.
Bugeaud, Yann
and
Pejković, Tomislav
2015.
Quadratic approximation in ℚp.
International Journal of Number Theory,
Vol. 11,
Issue. 01,
p.
193.
Pollington, Andrew
2017.
Number Theory with an Emphasis on the Markoff Spectrum.
p.
207.
Ooto, Tomohiro
2018.
On Diophantine exponents for Laurent series over a finite field.
Journal of Number Theory,
Vol. 185,
Issue. ,
p.
349.




 for the supremum of the exponents
for the supremum of the exponents