Article contents
The number of plane trees
Published online by Cambridge University Press: 26 February 2010
Extract
By a plane tree or rooted plane tree is meant a realization of a tree or rooted tree by points and arcs in the plane. By an isomorphism between two plane trees or rooted plane trees is meant an isomorphism in the usual sense for such trees which preserves the clockwise cyclic order of the edges about each node. In [2] Harary, Prins, and Tutte demonstrate how Polya's Theorem may be used to obtain formal expressions for the enumerating functions for unrooted, rooted, and other species of plane trees. In the process they obtain the explicit formula
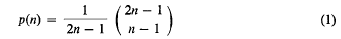
for the number of nonisomorphic planted plane trees with n ≥ 1 edges. (A planted tree is a rooted tree with root at a node of degree one.)
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1972
References
- 12
- Cited by


