Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T05:20:52.737Z Has data issue: false hasContentIssue false
  • English
  • Français

Note on a conjecture of L. A. Santaló

Published online by Cambridge University Press:  26 February 2010

H. G. Eggleston
H. G. Eggleston
Affiliation:
Bedford College, Regent's Park, London, N.W.1.
Get access

Extract

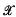Let be a plane bounded convex set whose width in the direction φ is 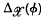. It has been shown by L. A. Santaló that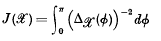

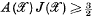is invariant under unimodular affine transformations. Santaló [1] established a number of properties of this invariant and conjectured that if the area of is A() then and that equality characterizes triangles. In this note Santaló's conjecture is shown to be true.

Type
Research Article
Information
Mathematika , Volume 8 , Issue 1 , June 1961 , pp. 63 - 65
Copyright
Copyright © University College London 1961

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Santaló, L. A., “A new affine invariant of plane and solid convex bodies”, Math. Notae, 16 (1937–38) (Spanish); reviewed in Math. Rev. No. 6567.Google Scholar
2.Ohmann, P., “Extremal probleme für konvexe Bereiche der euklidiscken Ebene”, Math. Zeit., 55 (1951–52), 346–352.CrossRefGoogle Scholar
A reference is given to the dissertation of K. Günther (Marburg 1948). See also Sholander, M., Trans. Amer. Math. Soc., 73 (1952), 139–173.CrossRefGoogle Scholar