A mixed packing problem

Extract

Let Λ′ be a lattice in three dimensional space. Let G be any point and denote by Λ the “displaced lattice”, consisting of all points X + G where X ε Λ′. Suppose that a sphere of radius 1 is centred at each point of Λ and a sphere of radius R−l, where 1 < R ≤ 2, is centred at each point of Λ′. If the lattice Λ′ and the point G are such that no two spheres of the system overlap we shall call Λ a mixed packing lattice, and shall denote its determinant by d(Λ) = d(Λ′). Let Δ be the lower bound of d(Λ) taken over all mixed packing lattices Λ. It can easily be proved that this is an attained lower bound, and any mixed packing lattice Λ, having d(Λ) = Δ, will be called a critical mixed packing lattice. We prove that

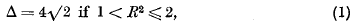
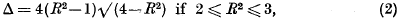
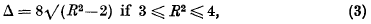
and shall describe, in Lemmas 1–3, the critical mixed packing lattices.