Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-28T10:19:55.877Z Has data issue: false hasContentIssue false
  • English
  • Français

The measure of the s-skeleton of a convex body

Published online by Cambridge University Press:  26 February 2010

G. R. Burton
G. R. Burton
Affiliation:
University College London.
Get access

Extract

When K is a convex body in d-dimensional euclidean space E and 0 ≤ s ≤ d, the s-skeleton of K, denoted skel(s)K, consists of those points of K which are not centres of (s + l)-dimensional balls contained in K. The s-skeleton is thus the union of the extreme faces of K having dimension at most s. The s-skeleton is a 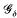-set [see 6] and it is therefore measurable with respect to the s-dimensional Hausdorff measure ℋ(s) [see 7]; here we normalize ℋ(s) so that it assigns unit measure to the s-dimensional unit cube.

Type
Research Article
Information
Mathematika , Volume 26 , Issue 2 , December 1979 , pp. 290 - 301
Copyright
Copyright © University College London 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Dalla, Leoni. PhD Thesis (University of London), in preparation.Google Scholar
2.Dalla, Leoni and Larman, D. G.. “Convex bodies with almost all k-dimensional sections polytopes”, Math. Proc. Camb. Phil. Soc., to appear.Google Scholar
3.Eggleston, H. G., Griinbaum, B. and Klee, V. L.. “Some semicontinuity theorems for convex polytopes and cell complexes”, Comment. Math. Helv., 39 (1964), 165–188.Google Scholar
4.Ewald, G., Larman, D. G. and Rogers, C. A.. “The directions of the line segments and of the r-dimensional balls on the boundary of a convex body in euclidean space”, Mathematika, 17 (1970), 1–20.CrossRefGoogle Scholar
5.Federer, H.. Geometric Measure Theory (Springer-Verlag, New York, 1969).Google Scholar
6.Larman, D. G. and Rogers, C. A.. “The finite dimensional skeletons of a compact convex set”, Bull London Math. Soc., 5 (1973), 145–153.Google Scholar
7.Rogers, C. A.. Hausdorjf Measures (Cambridge University Press, London, 1970).Google Scholar
8.Schneider, R.. “On the skeletons of convex bodies”, Bull. London Math. Soc., 10 (1978) 84–85.Google Scholar
9.Schneider, R., “Boundary structure and curvature of convex bodies”, Beitrdge zur Geometrie (Birkhauser-Verlag, Basel, 1979).Google Scholar