Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T05:37:37.660Z Has data issue: false hasContentIssue false
  • English
  • Français

MATRIX PROGRESSIONS IN MULTIDIMENSIONAL SETS OF INTEGERS

Part of: Sequences and sets

Published online by Cambridge University Press:  13 August 2014

Sean Prendiville
Sean Prendiville*
Affiliation:
Department of Mathematics and Statistics, University of Reading, Whiteknights, PO Box 220, Reading, RG6 6AX, U.K. email [email protected]
Get access

Abstract

We obtain density estimates for subsets of the $n$-dimensional integer lattice lacking four-term matrix progressions. As a consequence, we show that a subset of the grid 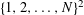$\{1,2,\dots ,N\}^{2}$ lacking four corners in a square has size at most 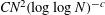$\mathit{CN}^{2}(\log \log N)^{-c}$. Our proofs involve the density increment method of Roth [J. London Math. Soc.28 (1953), 104–109] and Gowers [Geom. Funct. Anal.11(3) (2001), 465–588], together with the 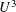$U^{3}$-inverse theorem of Green and Tao [Proc. Edinb. Math. Soc. (2) 51(1) (2008), 73–153].

MSC classification

Primary: 11B30: Arithmetic combinatorics; higher degree uniformity
Type
Research Article
Information
Mathematika , Volume 61 , Issue 1 , January 2015 , pp. 14 - 48
Copyright
Copyright © University College London 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Croot, E. S. III and Lev, V. F., Open problems in additive combinatorics. In Additive Combinatorics (CRM Proceedings and Lecture Notes 43), American Mathematical Society (Providence, RI, 2007), 207–233.CrossRefGoogle Scholar
Furstenberg, H. and Katznelson, Y., An ergodic Szemerédi theorem for commuting transformations. J. Anal. Math. 34 1978, 275–291.Google Scholar
Gowers, W. T., A new proof of Szemerédi’s theorem for arithmetic progressions of length four. Geom. Funct. Anal. 8(3) 1998, 529–551.Google Scholar
Gowers, W. T., A new proof of Szemerédi’s theorem. Geom. Funct. Anal. 11(3) 2001, 465–588.Google Scholar
Green, B. J., Finite field models in additive combinatorics. In Surveys in Combinatorics 2005 (London Mathematical Society Lecture Note Series 327), Cambridge University Press (Cambridge, 2005), 1–27.Google Scholar
Green, B. J. and Tao, T., An inverse theorem for the Gowers U 3(G) norm. Proc. Edinb. Math. Soc. (2) 51(1) 2008, 73–153.CrossRefGoogle Scholar
Green, B. J. and Tao, T., New bounds for Szemerédi’s theorem. II. A new bound for r 4(N). In Analytic Number Theory, Cambridge University Press (Cambridge, 2009), 180–204.Google Scholar
Heath-Brown, D. R., Integer sets containing no arithmetic progressions. J. Lond. Math. Soc. (2) 35(3) 1987, 385–394.Google Scholar
Roth, K. F., On certain sets of integers. J. Lond. Math. Soc. 28 1953, 104–109.Google Scholar
Roth, K. F., On certain sets of integers. II. J. Lond. Math. Soc. 29 1954, 20–26.CrossRefGoogle Scholar
Sanders, T., On Roth’s theorem on progressions. Ann. of Math. (2) 174(1) 2011, 619–636.Google Scholar
Schmidt, W. M., Small Fractional Parts of Polynomials (Regional Conference Series in Mathematics 32), American Mathematical Society (Providence, RI, 1977).Google Scholar
Shkredov, I. D., On a generalization of Szemerédi’s theorem. Proc. Lond. Math. Soc. (3) 93(3) 2006, 723–760.Google Scholar
Shkredov, I. D., On a two-dimensional analogue of Szemerédi’s theorem in abelian groups. Izv. Ross. Akad. Nauk Ser. Mat. 73(5) 2009, 181–224.Google Scholar
Szemerédi, E., Integer sets containing no arithmetic progressions. Acta Math. Hungar. 56(1–2) 1990, 155–158.CrossRefGoogle Scholar