Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bollauf, Maiara F.
Vaishampayan, Vinay A.
and
Costa, Sueli I. R.
2021.
On Communication for Distributed Babai Point Computation.
IEEE Transactions on Information Theory,
Vol. 67,
Issue. 10,
p.
6408.


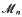 . This is then used to prove that a Minkowski reduced basis of a lattice of dimension
. This is then used to prove that a Minkowski reduced basis of a lattice of dimension 