Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-30T19:43:33.957Z Has data issue: false hasContentIssue false
  • English
  • Français

LEVEL SETS OF THE RESOLVENT NORM OF A LINEAR OPERATOR REVISITED

Part of: General theory of linear operators Groups and semigroups of linear operators, their generalizations and applications

Published online by Cambridge University Press:  26 June 2015

E. Brian Davies  and
Eugene Shargorodsky
E. Brian Davies
Affiliation:
Department of Mathematics, King’s College London, Strand, London WC2R 2LS, U.K. email [email protected]
Eugene Shargorodsky
Affiliation:
Department of Mathematics, King’s College London, Strand, London WC2R 2LS, U.K. email [email protected]
Get access

Abstract

It is proved that the resolvent norm of an operator with a compact resolvent on a Banach space 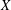$X$ cannot be constant on an open set if the underlying space or its dual is complex strictly convex. It is also shown that this is not the case for an arbitrary Banach space: there exists a separable, reflexive space 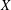$X$ and an unbounded, densely defined operator acting in 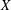$X$ with a compact resolvent whose norm is constant in a neighbourhood of zero; moreover 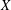$X$ is isometric to a Hilbert space on a subspace of co-dimension 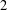$2$. There is also a bounded linear operator acting on the same space whose resolvent norm is constant in a neighbourhood of zero. It is shown that similar examples cannot exist in the co-dimension 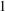$1$ case.

MSC classification

Primary: 47A10: Spectrum, resolvent
Secondary: 47D06: One-parameter semigroups and linear evolution equations
Type
Research Article
Information
Mathematika , Volume 62 , Issue 1 , 2016 , pp. 243 - 265
Copyright
Copyright © University College London 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arendt, W., Batty, C. J. K., Hieber, M. and Neubrander, F., Vector-valued Laplace Transforms and Cauchy Problems, Birkhäuser (Basel, 2011).CrossRefGoogle Scholar
Bauer, F. L., Stoer, J. and Witzgall, C., Absolute and monotonic norms. Numer. Math. 3 1961, 257–264.CrossRefGoogle Scholar
Bögli, S. and Siegl, P., Remarks on the convergence of pseudospectra. Integral Equations Operator Theory 80 2014, 303–321.CrossRefGoogle Scholar
Bonsall, F. F. and Duncan, J., Numerical Ranges II, Cambridge University Press (Cambridge, 1973).CrossRefGoogle Scholar
Böttcher, A., Pseudospectra and singular values of large convolution operators. J. Integral Equations Appl. 6 1994, 267–301.CrossRefGoogle Scholar
Böttcher, A. and Grudsky, S. M., Can spectral value sets of Toeplitz band matrices jump? Linear Algebra Appl. 351/352 2002, 99–116.CrossRefGoogle Scholar
Böttcher, A. and Grudsky, S. M., Spectral Properties of Banded Toeplitz Matrices, SIAM (Philadelphia, 2005).CrossRefGoogle Scholar
Böttcher, A., Grudsky, S. and Silbermann, B., Norms of inverses, spectra, and pseudospectra of large truncated Wiener–Hopf operators and Toeplitz matrices. New York J. Math. 3 1997, 1–31.Google Scholar
Butzer, P. L. and Berens, H., Semi-groups of Operators and Approximation, Springer (Berlin–Heidelberg–New York, 1967).CrossRefGoogle Scholar
Carothers, N. L., A Short Course on Banach Space Theory, Cambridge University Press (Cambridge, 2005).Google Scholar
Certain, M. W. and Kurtz, T. G., Landau–Kolmogorov inequalities for semigroups and groups. Proc. Amer. Math. Soc. 63 1977, 226–230.CrossRefGoogle Scholar
Clarkson, J., Uniformly convex spaces. Trans. Amer. Math. Soc. 40 1936, 396–414.CrossRefGoogle Scholar
Davies, E. B., Linear Operators and their Spectra, Cambridge University Press (Cambridge, 2007).CrossRefGoogle Scholar
Diestel, J., Geometry of Banach Spaces. Selected Topics, Springer (Berlin–Heidelberg–New York, 1975).CrossRefGoogle Scholar
Dowling, P. N. and Turett, B., Complex strict convexity of absolute norms on ℂn and direct sums of Banach spaces. J. Math. Anal. Appl. 323 2006, 930–937.CrossRefGoogle Scholar
Dunford, N. and Schwartz, J. T., Linear Operators. I. General Theory, Interscience Publishers (New York and London, 1958).Google Scholar
Gallestey, E., Hinrichsen, D. and Pritchard, A. J., Spectral value sets of closed linear operators. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 456 2000, 1397–1418.Google Scholar
Globevnik, J., On complex strict and uniform convexity. Proc. Amer. Math. Soc. 47 1975, 175–178.CrossRefGoogle Scholar
Globevnik, J., Norm-constant analytic functions and equivalent norms. Illinois J. Math. 20 1976, 503–506.CrossRefGoogle Scholar
Globevnik, J. and Vidav, I., On operator-valued analytic functions with constant norm. J. Funct. Anal. 15 1974, 394–403.CrossRefGoogle Scholar
Hille, E. and Phillips, R. S., Functional Analysis and Semigroups, American Mathematical Society (Providence, RI, 1957).Google Scholar
Horn, R. A. and Johnson, C. R., Matrix Analysis, Cambridge University Press (Cambridge, 2013).Google Scholar
Kallman, R. R. and Rota, G.-C., On the inequality ∥f ′∥2⩽4∥f∥⋅∥f ′′∥. In Inequalities 2, Proc. 2nd Sympos. Inequalities, U.S. Air Force Acad., Colorado 1967, (1970), 187–192.Google Scholar
Kato, T., Perturbation Theory for Linear Operators, Springer (New York, 1966).Google Scholar
Kato, M., Saito, K.-S. and Tamura, T., On 𝜓-direct sums of Banach spaces and convexity. J. Aust. Math. Soc. 75 2003, 413–422.CrossRefGoogle Scholar
Kolmogorov, A. N., On inequalities between the upper bounds of the successive derivatives of an arbitrary function on an infinite interval. Učen. Zap. Moskov. Gos. Univ. Mat. 30 1939, 3–13; Engl. transl., Amer. Math. Soc. Transl. 2(1) (1962), 233–243.Google Scholar
Lancaster, P. and Farahat, H. K., Norms on direct sums and tensor products. Math. Comput. 26 1972, 401–414.CrossRefGoogle Scholar
Landau, E., Einige Ungleichungen für zweimal differenzierbare Funktionen. Proc. Lond. Math. Soc. (2) 13 1913, 43–49.Google Scholar
Lešnjak, G., Complex convexity and finitely additive vector measures. Proc. Amer. Math. Soc. 102 1988, 867–873.CrossRefGoogle Scholar
Pazy, A., Semigroups of Linear Operators and Applications to Partial Differential Equations, Springer (New York, 1983).CrossRefGoogle Scholar
Saito, K.-S. and Kato, M., Uniform convexity of 𝜓-direct sums of Banach spaces. J. Math. Anal. Appl. 277 2003, 1–11.CrossRefGoogle Scholar
Schoenberg, I. J. and Cavaretta, A., Solution of Landau’s Problem concerning Higher Derivatives on the Halfline (MRC T.S.R. 1060), University of Wisconsin–Madison Mathematics Research Center (Madison, WI, 1970).Google Scholar
Shargorodsky, E., On the level sets of the resolvent norm of a linear operator. Bull. Lond. Math. Soc. 40 2008, 493–504.CrossRefGoogle Scholar
Shargorodsky, E., Pseudospectra of semigroup generators. Bull. Lond. Math. Soc. 42 2010, 1031–1034.CrossRefGoogle Scholar
Shargorodsky, E. and Shkarin, S., The level sets of the resolvent norm and convexity properties of Banach spaces. Arch. Math. 93 2009, 59–66.CrossRefGoogle Scholar
Takahashi, Y., Kato, M. and Saito, K.-S., Strict convexity of absolute norms on ℂ2 and direct sums of Banach spaces. J. Inequal. Appl. 7 2002, 179–186.Google Scholar
Trefethen, L. N., Pseudospectra of linear operators. SIAM Rev. 39 1997, 383–406.CrossRefGoogle Scholar
Trefethen, L. N. and Embree, M., Spectra and Pseudospectra: the Behavior of Nonnormal Matrices and Operators, Princeton University Press (Princeton, NJ, 2005).CrossRefGoogle Scholar