Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hazewinkel, Michiel
2000.
Encyclopaedia of Mathematics.
p.
141.
Beresnevich, V.
and
Velani, S.
2009.
Classical Metric Diophantine Approximation Revisited: The Khintchine-Groshev Theorem.
International Mathematics Research Notices,
Haynes, A. K.
2009.
The Metric Theory of p-Adic Approximation.
International Mathematics Research Notices,
Haynes, Alan K.
Pollington, Andrew D.
and
Velani, Sanju L.
2012.
The Duffin–Schaeffer Conjecture with extra divergence.
Mathematische Annalen,
Vol. 353,
Issue. 2,
p.
259.
Waldschmidt, Michel
2012.
Number Theory, Analysis and Geometry.
p.
659.
Narkiewicz, Władysław
2012.
Rational Number Theory in the 20th Century.
p.
131.
Li, Liangpan
2013.
ZERO‐ONE LAWS IN SIMULTANEOUS AND MULTIPLICATIVE DIOPHANTINE APPROXIMATION.
Mathematika,
Vol. 59,
Issue. 2,
p.
321.
Beresnevich, Victor
Harman, Glyn
Haynes, Alan
and
Velani, Sanju
2013.
The Duffin–Schaeffer conjecture with extra divergence II.
Mathematische Zeitschrift,
Vol. 275,
Issue. 1-2,
p.
127.
DODSON, MAURICE
and
EVERITT, BRENT
2014.
Metrical Diophantine approximation for quaternions.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 157,
Issue. 3,
p.
513.
WANG, BAO-WEI
WU, JUN
and
XU, JIAN
2015.
Mass transference principle for limsup sets generated by rectangles.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 158,
Issue. 3,
p.
419.
Palmer, Matthew
2015.
Diagonal approximation in completions of Q.
Journal of Number Theory,
Vol. 147,
Issue. ,
p.
109.
Li, Liangpan
2016.
THE DUFFIN–SCHAEFFER‐TYPE CONJECTURES IN VARIOUS LOCAL FIELDS.
Mathematika,
Vol. 62,
Issue. 3,
p.
753.
Ramírez, Felipe A.
2017.
Counterexamples, covering systems, and zero-one laws for inhomogeneous approximation.
International Journal of Number Theory,
Vol. 13,
Issue. 03,
p.
633.
Aistleitner, Christoph
Lachmann, Thomas
Munsch, Marc
Technau, Niclas
and
Zafeiropoulos, Agamemnon
2019.
The Duffin-Schaeffer conjecture with extra divergence.
Advances in Mathematics,
Vol. 356,
Issue. ,
p.
106808.
MA, CHAO
and
ZHANG, SHAOHUA
2019.
JARNÍK’S THEOREM WITHOUT THE MONOTONICITY ON THE APPROXIMATING FUNCTION.
Fractals,
Vol. 27,
Issue. 04,
p.
1950044.
LIU, WENCAI
2019.
SOME REFINED RESULTS ON THE MIXED LITTLEWOOD CONJECTURE FOR PSEUDO-ABSOLUTE VALUES.
Journal of the Australian Mathematical Society,
Vol. 107,
Issue. 1,
p.
91.
Ramírez, Felipe A.
2020.
KHINTCHINE'S THEOREM WITH RANDOM FRACTIONS.
Mathematika,
Vol. 66,
Issue. 1,
p.
178.
Kaziulytė, Laima
2020.
Variants of Khintchine's theorem in metric Diophantine approximation.
Journal of Number Theory,
Vol. 215,
Issue. ,
p.
160.
Kristensen, Simon
and
Laursen, Mathias Løkkegaard
2023.
The $p$-adic Duffin-Schaeffer conjecture.
Functiones et Approximatio Commentarii Mathematici,
Vol. 68,
Issue. 1,
Granville, Andrew
2023.
Missing digits and good approximations.
Bulletin of the American Mathematical Society,


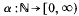 the statement;
the statement;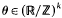 there are infinitely many natural numbers
there are infinitely many natural numbers 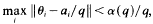
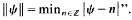
 diverges.
diverges.