Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-24T22:31:23.539Z Has data issue: false hasContentIssue false
  • English
  • Français

Irrationality of lattices in finite characteristic

Published online by Cambridge University Press:  26 February 2010

Jing Yu
Jing Yu
Affiliation:
Institute of Mathematics, Academia Sinica, Nankang, Taipei, Taiwan, Republic of China
Get access

Extract

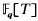Let q = pn, p a rational prime, and let be the finite field with q elements. The polynomial ring is considered as an analogue of the ring of rational integers ℤ. Completing the quotient field with respect to the normalized valuation at ∞, and then taking algebraic closure, we obtained the field k∞ whose elements will be called “numbers”.

Type
Research Article
Information
Mathematika , Volume 29 , Issue 2 , December 1982 , pp. 227 - 230
Copyright
Copyright © University College London 1982

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

C.Carlitz, L.. On certain functions connected with polynomials in a Galois field. Duke Math. J., 1 (1935), 137–168.CrossRefGoogle Scholar
D.Drinfeld, V. G.. Elliptic Modules (Russian). Math. Sbornik 94 (1974), 594–627. English translation, Math. USSR Sbornik, 23 (1974), No. 4.Google Scholar
G.Goss, D.. Von Staudt for Fq,[T]. Duke Math. J., 45 (1978), 885910.CrossRefGoogle Scholar
S.Siegel, C. L.. Transcendental numbers, Annals of Math. Studies 16, (Princeton, 1949).Google Scholar
W.Wade, L. I.. Certain quantities transcendental over GF(pn, x). Duke Math. J., 8 (1941), 701–720.CrossRefGoogle Scholar