Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Br�ndsted, Arne
1978.
Barrier cones and intersections of translates of convex sets.
Archiv der Mathematik,
Vol. 30,
Issue. 1,
p.
99.
Br�ndsted, Arne
1978.
More about intersections of translates of convex sets.
Archiv der Mathematik,
Vol. 31,
Issue. 1,
p.
620.
Coquet, G.
and
Dupin, J. C.
1979.
On families of convex sets having the constant intersection property.
Archiv der Mathematik,
Vol. 33,
Issue. 1,
p.
172.


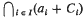 is non-empty for all families (
is non-empty for all families (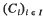 to have the intersection property.
to have the intersection property.