Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-27T06:40:53.338Z Has data issue: false hasContentIssue false
  • English
  • Français

Indefinite quadratic forms in many variables

Published online by Cambridge University Press:  26 February 2010

B. J. Birch  and
H. Davenport
B. J. Birch
Affiliation:
Graduate College, Princeton, N.J.
H. Davenport
Affiliation:
University College, London.
Get access

Extract

Let Q(x1, …, xn) be an indefinite quadratic form in n variables with real coefficients. It is conjectured that, provided n ≥ 5, the inequality

is soluble for every ε > 0 in integers x1, …, xn, not all 0. The first progress towards proving this conjecture was made by Davenport in two recent papers; the result obtained involved, however, a condition on the type of the form as well as on n. We say that a non-singular Q is of type (r, n—r) if, when Q is expressed as a sum of squares of n real linear forms with positive and negative signs, there are r positive signs and n—r negative signs. It was proved that (1) is always soluble provided that

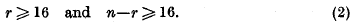
Type
Research Article
Information
Mathematika , Volume 5 , Issue 1 , June 1958 , pp. 8 - 12
Copyright
Copyright © University College London 1958

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

page 8 note * Mathematika, 3 (1956), 81–101;CrossRefGoogle ScholarProc. London Math. Soc. (3), 8 (1958), 109–126.Google Scholar

page 8 note † Proc. Cambridge Phil. Soc, 51 (1955), 262–264CrossRefGoogle Scholar and 52 (1956), 604.

page 9 note * Bull. American Math. Soc., 51 (1945), 749–755.CrossRefGoogle Scholar

page 9 note † Journal London Math. Soc., 21 (1946), 185–193.Google Scholar

page 9 note ‡ Proc. Cambridge Phil. Soc., 54 (1958), 135–138.CrossRefGoogle Scholar

page 9 note § Mathematika, 4 (1957), 102–105.CrossRefGoogle Scholar