Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Furuta, Yoshiomi
1967.
The Genus Field and Genus Number in Algebraic Number Fields.
Nagoya Mathematical Journal,
Vol. 29,
Issue. ,
p.
281.
Demushkin, S. P.
1971.
Progress in Mathematics.
p.
59.
Shirai, Susumu
1978.
On the central class field mod of Galois extensions of an algebraic number field.
Nagoya Mathematical Journal,
Vol. 71,
Issue. ,
p.
61.
Cornell, Gary
1982.
On the construction of relative genus fields.
Transactions of the American Mathematical Society,
Vol. 271,
Issue. 2,
p.
501.
Iimura, K.
1986.
Principal factors in a pure cubic field and its unramified cyclic cubic extensions.
Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg,
Vol. 56,
Issue. 1,
p.
115.
Maldonado-Ramírez, Myriam
Rzedowski-Calderón, Martha
and
Villa-Salvador, Gabriel
2017.
Genus fields of congruence function fields.
Finite Fields and Their Applications,
Vol. 44,
Issue. ,
p.
56.
Barreto-Castaneda, Jonny Fernando
Montelongo-Vazquez, Carlos
Reyes-Morales, Carlos Daniel
Rzedowski-Calderon, Martha
and
Villa-Salvador, Gabriel
2018.
Genus fields of abelian extensions of rational congruence function fields, II.
Rocky Mountain Journal of Mathematics,
Vol. 48,
Issue. 7,
Rzedowski‐Calderón, Martha
and
Villa‐Salvador, Gabriel
2023.
Class fields, Dirichlet characters, and extended genus fields of global function fields.
Mathematische Nachrichten,
Vol. 296,
Issue. 8,
p.
3606.
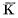 , of K, which is defined as the maximal non-ramified extension of K composed of K and of some absolutely Abelian field.
, of K, which is defined as the maximal non-ramified extension of K composed of K and of some absolutely Abelian field.