Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T05:01:34.915Z Has data issue: false hasContentIssue false
  • English
  • Français

A GENERALIZATION OF THE DISCRETE VERSION OF MINKOWSKI’S FUNDAMENTAL THEOREM

Part of: Geometry of numbers Additive number theory; partitions Discrete geometry General convexity

Published online by Cambridge University Press:  29 February 2016

Bernardo González Merino  and
Matthias Henze
Bernardo González Merino
Affiliation:
Zentrum Mathematik, Technische Universität München, Boltzmannstr. 3, D-85747 Garching bei München, Germany email [email protected]
Matthias Henze
Affiliation:
Institut für Informatik, Freie Universität Berlin, Takustraße 9, D-14195 Berlin, Germany email [email protected]
Get access

Abstract

One of the most fruitful results from Minkowski’s geometric viewpoint on number theory is his so-called first fundamental theorem. It provides an optimal upper bound for the volume of a 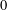$0$ -symmetric convex body whose only interior lattice point is the origin. Minkowski also obtained a discrete analog by proving optimal upper bounds on the number of lattice points in the boundary of such convex bodies. Whereas the volume inequality has been generalized to any number of interior lattice points already by van der Corput in the 1930s, a corresponding result for the discrete case remained to be proven. Our main contribution is a corresponding optimal relation between the number of boundary and interior lattice points of a 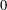$0$ -symmetric convex body. The proof relies on a congruence argument and a difference set estimate from additive combinatorics.

MSC classification

Primary: 52C07: Lattices and convex bodies in $n$ dimensions
Secondary: 11H06: Lattices and convex bodies 52A40: Inequalities and extremum problems 11P70: Inverse problems of additive number theory, including sumsets 52A20: Convex sets in $n$ dimensions (including convex hypersurfaces)
Type
Research Article
Information
Mathematika , Volume 62 , Issue 3 , 2016 , pp. 637 - 652
Copyright
Copyright © University College London 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aliev, I., Bassett, R., De Loera, J. A. and Louveaux, Q., A quantitative Doignon–Bell–Scarf theorem. Combinatorica (to appear), arXiv:1405.2480.Google Scholar
Averkov, G., On maximal S-free sets and the Helly number for the family of S-convex sets. SIAM J. Discrete Math. 27(3) 2013, 1610–1624.Google Scholar
Averkov, G., Krümpelmann, J. and Nill, B., Largest integral simplices with one interior integral point: solution of Hensley’s conjecture and related results. Adv. Math. 274 2015, 118–166.Google Scholar
Averkov, G. and Weismantel, R., Transversal numbers over subsets of linear spaces. Adv. Geom. 12(1) 2012, 19–28.Google Scholar
Betke, U., Henk, M. and Wills, J. M., Successive-minima-type inequalities. Discrete Comput. Geom. 9(2) 1993, 165–175.Google Scholar
van der Corput, J. G., Verallgemeinerung einer Mordellschen Beweismethode in der Geometrie der Zahlen II. Acta Arith. 2 1936, 145–146.Google Scholar
Doignon, J.-P., Convexity in cristallographical lattices. J. Geom. 3 1973, 71–85.Google Scholar
Draisma, J., McAllister, T. B. and Nill, B., Lattice-width directions and Minkowski’s 3 d -theorem. SIAM J. Discrete Math. 26(3) 2012, 1104–1107.Google Scholar
Freiman, G. A., Heppes, A. and Uhrin, B., A lower estimation for the cardinality of finite difference sets in R n . In Number Theory, Vol. I (Budapest, 1987) (Colloquium Mathematical Society János Bolyai 51 ), Amsterdam (North-Holland, 1990), 125–139.Google Scholar
Gruber, P. M., Convex and Discrete Geometry (Grundlehren der Mathematischen Wissenschaften 336 ), Springer (Berlin, 2007).Google Scholar
Gruber, P. M. and Lekkerkerker, C. G., Geometry of Numbers, 2nd edn., (North-Holland Mathematical Library 37 ), North-Holland (Amsterdam, 1987).Google Scholar
Malikiosis, R., A discrete analogue for Minkowski’s second theorem on successive minima. Adv. Geom. 12(2) 2012, 365–380.Google Scholar
Minkowski, H., Geometrie der Zahlen (Bibliotheca Mathematica Teubneriana, Teubner (Leipzig–Berlin, 1896), reprinted by Johnson Reprint Corp., New York, 1968.Google Scholar
Pikhurko, O., Lattice points in lattice polytopes. Mathematika 48(1–2) 2001, 15–24.Google Scholar
Rabinowitz, S., A theorem about collinear lattice points. Util. Math. 36 1989, 93–95.Google Scholar
Ruzsa, I. Z., Additive combinatorics and geometry of numbers. In Proceedings of the International Congress of Mathematicians, Vol. 3, European Mathematical Society (Zürich, 2006), 911–930.Google Scholar
Scott, P. R., On convex lattice polygons. Bull. Aust. Math. Soc. 15(3) 1976, 395–399.Google Scholar
Stanchescu, Y. V., On finite difference sets. Acta Math. Hungar. 79(1–2) 1998, 123–138.Google Scholar
Stanchescu, Y. V., An upper bound for d-dimensional difference sets. Combinatorica 21(4) 2001, 591–595.CrossRefGoogle Scholar
Tao, T. and Vu, V., Additive Combinatorics (Cambridge Studies in Advanced Mathematics 105 ), Cambridge University Press (Cambridge, 2006).Google Scholar