Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-25T11:44:41.356Z Has data issue: false hasContentIssue false
  • English
  • Français

A generalization of mixed invariant sets

Part of: Functions of several variables

Published online by Cambridge University Press:  26 February 2010

Uwe Feiste
Uwe Feiste
Affiliation:
Ernst-Moritz-Arndt-Universität Greifswald, Sektion Mathematik, Friedrich-Ludwig-Jahn-Straβe 15a, Greifswald, DDR-2200.
Get access

Summary

The concept of mixed invariant set is due to Bandt [1], Bedford [2], Dekking [3, 4], Marion [4] and Schulz [10]. An m-tuple B = (B1, …, Bm) of closed and bounded subsets Bi of a complete finitely compact (bounded and closed subsets are compact) metric space X is called a mixed invariant set with respect to contractions f1, …, fm and a transition matrix M = (mij), if, and only if,

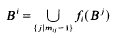
for every i ∈ {1, …, m}. In the papers quoted an essential condition is that all mappings f1, …, fm be contractions. We will show that, under certain conditions, the construction of mixed invariant sets also works in cases where some of the mappings are isometries or even expanding mappings.

MSC classification

Secondary: 26B99: None of the above, but in this section
Type
Research Article
Information
Mathematika , Volume 35 , Issue 2 , December 1988 , pp. 198 - 206
Copyright
Copyright © University College London 1988

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Ch. Bandt. Self-similar sets 1. Math. Nachr. (submitted). Self-similar sets 3. Preprint (Greifswald, 1987).Google Scholar
2.Bedford, T.. Dimension and dynamics for fractal recurrent sets. J. London Math. Soc. (2), 33 (1986), 89–100.CrossRefGoogle Scholar
3.Dekking, F. M.. Recurrent sets. Adv. in Math., 44 (1982), 78–104.CrossRefGoogle Scholar
4.Dekking, F. M.. Recurrent sets: A fractal formalism. Report 82–32 (Delft, 1982).Google Scholar
5.Falconer, K. J.. The geometry of fractal sets (Cambridge University Press, 1985).CrossRefGoogle Scholar
6.Hutchinson, J. E.. Fractals and self-similarity. Indiana Univ. Math. J., 30 (1981), 713–747.CrossRefGoogle Scholar
7.Marion, J.. Mesures de Hausdorff et theorie de Perron-Frobenius des matrices non-negatives. Ann. Inst. Fourier, Grenoble, 35, 4 (1985), 99–125.CrossRefGoogle Scholar
8.Mauldin, R. D. and Williams, S. C.. Random recursive construction asymptotic geometric and topological properties. Trans. Amer. Math. Soc., 29 (1986), 325–346.CrossRefGoogle Scholar
9.Moran, P. A. P.. Additive functions of intervals and Hausdorff measure. Proc. Cambridge Phil. Soc., 42 (1946), 15–23.CrossRefGoogle Scholar
10.Schulz, M.. Hausdorff-Dimension von Cantormengen mit Anwendungen auf Attraktoren. Dissertation (Humboldt-Universität Berlin, 1986).Google Scholar