Hostname: page-component-6bf8c574d5-956mj Total loading time: 0 Render date: 2025-02-17T18:21:15.683Z Has data issue: false hasContentIssue false
  • English
  • Français

FRACTIONAL PARTS OF POLYNOMIALS OVER THE PRIMES. II

Part of: Exponential sums and character sums Multiplicative number theory

Published online by Cambridge University Press:  26 June 2018

Roger Baker
Roger Baker*
Affiliation:
Department of Mathematics, Brigham Young University, Provo, UT 84602, U.S.A. email [email protected]
Get access

Abstract

Let 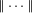$\Vert \cdots \Vert$ denote distance from the integers. Let $\unicode[STIX]{x1D6FC}$, 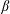$\unicode[STIX]{x1D6FD}$, 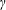$\unicode[STIX]{x1D6FE}$ be real numbers with $\unicode[STIX]{x1D6FC}$ irrational. We show that the inequality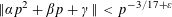

$$\begin{eqnarray}\Vert \unicode[STIX]{x1D6FC}p^{2}+\unicode[STIX]{x1D6FD}p+\unicode[STIX]{x1D6FE}\Vert <p^{-3/17+\unicode[STIX]{x1D700}}\end{eqnarray}$$
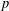has infinitely many solutions in primes $p$, sharpening a result due to Harman [On the distribution of $\unicode[STIX]{x1D6FC}p$ modulo one II. Proc. Lond. Math. Soc. (3)72 (1996), 241–260] in the case $\unicode[STIX]{x1D6FD}=0$ and Baker [Fractional parts of polynomials over the primes. Mathematika63 (2017), 715–733] in the general case.

MSC classification

Secondary: 11L20: Sums over primes 11N36: Applications of sieve methods
Type
Research Article
Information
Mathematika , Volume 64 , Issue 3 , 2018 , pp. 742 - 769
Copyright
Copyright © University College London 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research supported in part by Collaboration Grant 412557 from the Simons Foundation.

References

Baker, R. C., Fractional parts of polynomials over the primes. Mathematika 63 2017, 715–733.Google Scholar
Baker, R. C. and Harman, G., On the distribution of 𝛼p k modulo one. Mathematika 48 1991, 170–184.Google Scholar
Baker, R. C. and Weingartner, A., A ternary Diophantine inequality over primes. Acta Arith. 162 2014, 159–196.Google Scholar
Birch, B. J. and Davenport, H., On a theorem of Davenport and Heilbronn. Acta Math. 100 1958, 259–279.Google Scholar
Cheer, A. Y. and Goldston, D. A., A differential-delay equation arising from the sieve of Eratosthenes. Math. Comp. 55 1990, 129–141.Google Scholar
Ghosh, A., The distribution of 𝛼p 2 modulo 1. Proc. Lond. Math Soc. (3) 42 1981, 252–269.Google Scholar
Harman, G., On the distribution of 𝛼p modulo one II. Proc. Lond. Math. Soc. (3) 72 1996, 241–260.Google Scholar
Harman, G., Prime-Detecting Sieves, Princeton University Press (Princeton, NJ, 2007).Google Scholar
Heath-Brown, D. R., Prime numbers in short intervals and a generalized Vaughan identity. Canad. J. Math. 34 1982, 1365–1377.Google Scholar
Iwaniec, H., A new form of the error term in the linear sieve. Acta Arith. 37 1980, 307–320.Google Scholar
Vinogradov, I. M., On the estimate of trigonometric sums with prime numbers. Izv. Akad. Nauk. SSSR Ser. Mat. 12 1948, 225–248.Google Scholar